Question: Let A be an n x n matrix with eigenvalues M1 = 1 and = 12 = -1 and corresponding eigenvectors v, and v2, respectively.

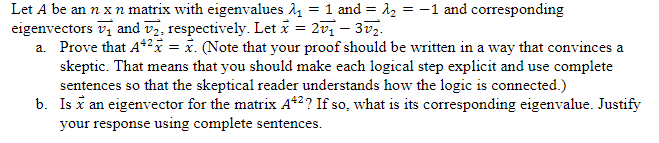
Let A be an n x n matrix with eigenvalues M1 = 1 and = 12 = -1 and corresponding eigenvectors v, and v2, respectively. Let x = 2v1 - 3v2. a. Prove that A* x = x. (Note that your proof should be written in a way that convinces a skeptic. That means that you should make each logical step explicit and use complete sentences so that the skeptical reader understands how the logic is connected.) b. Is x an eigenvector for the matrix A*? If so, what is its corresponding eigenvalue. Justify your response using complete sentences

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let A be a 2 x 2 matrix with eigenvalues 2 and 1/2 with corresponding eigenvectors V1 = and v2 For the discrete dynamical system Xk+1 = Axe, classify the origin as an attractor, repeller, or...

Midterm Review 1. Let A be an 'n, X n matrix with eigenvalues A1, . . . , A" and corresponding eigenvectors 171, . . . ,5\". (a) Give the eigenvalues of A2 | A + In where In is the n X n identity...

Please help me with parts (d) and (e), thanks. Eigenvectors and Diagonalization (a) Let A be an n x n matrix with n linearly independent eigenvectors 71, 72, ..., Un, and corre- sponding eigenvalues...

11. Solve the following system X = X + 3 4 subject to the initial condition X (0) = 5 13et - 8e2t - 9 Ans: X = 13et + 12e2t + 6 12. (January 2006) (a) Solve the initial value problem X' = X, with...

1) Which of the following statements are correct? a) A square matrix A is not invertible if and only if A = 0 is an eigenvalue of A. b) If v and v2 are linearly independent eigenvectors of a matrix...

(1 point) Let M be a 2 x 2 matrix with eigenvalues 11 = 0.3, 12 = 0.25 with corresponding eigenvectors Consider the difference equation XK+1 = MXk with initial condition X = W N Write the initial...

Please help me with (b) and (c), thank you! Part (a) solution: Eigenvectors and Diagonalization (a) Let A be an n x n matrix with n linearly independent eigenvectors 71, 72, ..., Un, and corre-...

1. Let A = 90 3 552 Find the characteristic polynomial of A and guess one of its roots by looking at integer divisors of the constant term. Find an eigenvector corresponding to this eigenvalue, and...

Let A be a 2 x 2 matrix with eigenvalues 4 and - and corresponding eigenvectors v, = and v2 = . Let 4Xk be a solution of the difference equation XK +1 = AXk, XO 121 a. Compute x1 = Axo. [Hint: You do...

(a) Let A and B be two square matrices of the same dimension and A be an invertible matrix then (A-1BA) 2020 = A-1 B2020 A. O True False Justification: (b) Let A be an n x n matrix. The set of all n...

Consider the observations x 1 , x 2 ,...,x n from the gamma distribution discussed in Section 6.6. (a) Write out the likelihood function. (b) Write out a set of equations which when solved give the...

If y^2 = 5x2 +5 then find d^2y/dx^2 at the point (-2,-5) in simplest form.

HRL is considering the following change: The firm will recapitalize by setting the new D / V ratio to one 3 / 4 of the original value ( i . e . New D / V = 0 . 7 5 * Old D / V ) . Cost of Debt ( RD )...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...