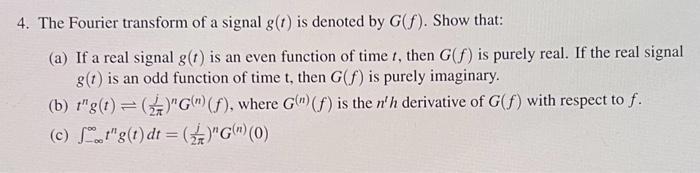
4. The Fourier transform of a signal g(t) is denoted by G(f). Show that: (a) If a real signal g(t) is an even function of time t, then G(f) is purely real. If the real signal g(t) is an odd function of time t, then G(f) is purely imaginary. (b) 1"g(t)=()"G(") (f), where G(") (f) is the n'h derivative of G(f) with respect to f. (c) "g(t)dt = ()"G(") (0)