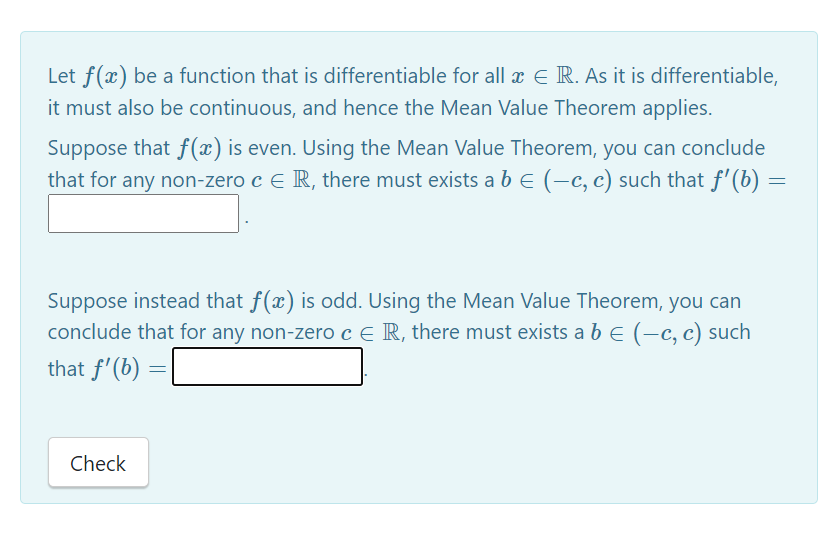
Let at) be a function that is differentiable for all at: E R. As it is differentiable, it must also be continuous, and hence the Mean Value Theorem applies. Suppose that f(':) is even. Using the Mean Value Theorem, you can conclude that for any non-zero c E R, there must exists a b E (c, e) such that f'(b) : :- Suppose instead that at) is odd. Using the Mean Value Theorem, you can conclude that for any non-zero c 6 IR, there must exists a b E (c, c) such mar