Question: Let be a positive number. The continuous random variable X is called exponential with parameter when its probability density function is (a) Find

Let λ be a positive number. The continuous random variable X is called exponential with parameter λ when its probability density function is

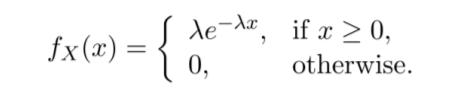
Let λ be a positive number. The continuous random variable X is

(a) Find the cumulative distribution function (CDF) of X.

(b) Find the mean of X.

(c) Find the variance of X.

(d) Suppose X1, X2, and X3 are independent exponential random variables, each with parameter λ. Find the PDF of Z = max{X1, X2, X3}.

(e) Find the PDF of W = min{X1, X2}.

Step by Step Solution

★★★★★

3.34 Rating (148 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

To solve the problem well work through each part stepbystep a Find the Cumulative Distribution Funct... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

The probability density of the continuous random variable X is given by (a) Draw its graph and verify that the total area under the curve (above the x- axis) is equal to 1. (b) Find P(3

Q:

The PDF of a continuous random variable X is as follows: f(X) = c(4x - 2x2) 0 x 2 = 0 otherwise a. For this to be a proper density function, what must be the value of c? b. Find P(l

Q:

The probability distribution of the discrete random variable x is p(x) = krx, 0

Q:

Accidental poisoning of children is a great concern to the Poison Control Center. From the past, 12.5% of all children reported with accidental poisoning required hospitalization. For the years 1993...

Q:

Suppose that the random variable X has an exponential distribution with parameter ? > 0. (i) What are the probability density function, fX(x), and the probability distribution function, FX(x), for...

Q:

I need hint or answer of PROBLEM 3 a and b. PROBLEM 3 Answer the following questions: a. Suppose X1, X2, X3, X4 are i.i.d. random variables N(0, ). Let Q = X1X2 - X3X4. By finding the moment...

Q:

only do 12 (1) The probability that an "accident prone" policy holder has an accident within a year is 0.6, while the probability that a "non-accident prone" policyholder has an accident within a...

Q:

Only do (9)(10) (1) The probability that an "accident prone" policy holder has an accident within a year is 0.6, while the probability that a "non-accident prone" policyholder has an accident within...

Q:

Only do(7)(8) (1) The probability that an "accident prone" policy holder has an accident within a year is 0.6, while the probability that a "non-accident prone" policyholder has an accident within a...

Q:

CS 70 Discrete Mathematics and Probability Theory Fall 2017 Kannan Ramchandran and Satish Rao HW 12 Sundry Before you start your homework, write down your team. Who else did you work with on this...

Q:

Exercise 11-07 The stockholders' equity section of Bridgeport Corp.'s balance sheet at December 31 is presented here. BRIDGEPORT CORP. Balance Sheet (partial) Stockholders' equity Paid-in capital...

Q:

A hedger is short spot and long futures. Today, spot is 4.40 and the June future is 5.00. A bit later, spot goes to 5.00 and the June future goes to 5.10. What has happened to basis in this period?...

Q:

The EICAS CRTs (cathode ray tubes) are: Group of answer choices Identical Directly powered from the battery bus Cooled by AC-powered fans All the above Only b and c

Q:

A recruiter asks candidates for a customer service rep position, "Why are you interested in this role?" Which response ( s ) would hurt a candidate's chances of advancing to the next round? Select...

Q:

You are starting to draw up your plans for the program. You realize that employees are going to have a lot of questions about the change. You cannot get all of the questions handled in all - hands...

Q:

I need these charts filled in using the information given Instructions Analysis Ledger Trial Balance Greenwald and Mass developed a business and plan to begin by offering clinics for basic outdoor...

Q:

- the data communication rstandard of web pages. - Meaning of HTTP

Q:

What is the amount of total interest dollars earned on a $5,000 deposit earning 6% for 20 years?

Q:

If a person gets seven heads and three tails in 10 tosses of a balanced coin, find the probabilities for 2, 3, 4, 5, 6, and 7 runs.

Q:

With reference to Exercise 13.42, use suitable statistical software to find the P-value corresponding to the observed value of the test statistic. Use this P-value to rework the exercise. In exercise...

Q:

Perform multiple-range tests to characterize the differences among compressor designs and among regions in Example 15.3. Use the 0.05 level of significance.

Q:

Ms. Esperanto obtained a $40,000 home equity loan at 7.5% compounded monthly. a. What will she pay monthly if the amortization period is 15 years? b. How much of the payment made at the end of the...

Q:

Elkford Loggings bank will fix the interest rate on a $60,000 loan at 8.1% compounded monthly for the first four-year term of an eight-year amortization period. Monthly payments are required on the...

Q:

An interactive chart for investigating the composition of loan payments is provided in the textbooks Web site. In Chapter 14 of the Student Edition, find Composition of Loan Payments. The chart...