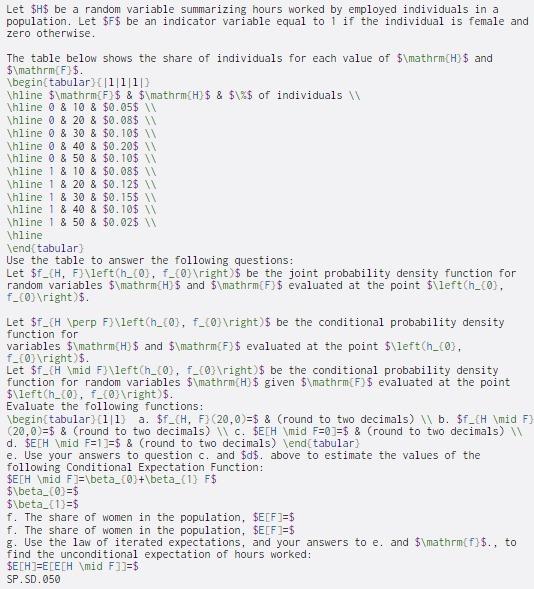
Let $$ be a random variable summarizing hours worked by employed individuals in a population. Let $F$ be an indicator variable equal to 1 if the individual is female and zero otherwise. The table below shows the share of individuals for each value of $\mathrm{H} $ and $\mathrm{F}$. \begin{tabular) 11/1/1) Vhline $\mathrm{F} $ & $\mathrm{H}$ & $\ $ of individuals \hline 0 & 10 & $0.05$ W Thline 0 & 20 & $0.08$ Thline 0 & 30 & $0.10$ Vhline 0 & 40 & $0.20$ \hline 0 & 50 & $0.10$ Whline 1 & 10 & $0.08$ \hline 1 & 20 & $0.12$ Thline 1 & 30 & $0.15$ Vhline 1 & 40 & $0.10$ \hline 1 & 50 & $0.02$ Whline \end{tabular Use the table to answer the following questions: Let $f_CH, F}\left(h_{0}, F_CO} ight)$ be the joint probability density function for random variables $\mathrm{H} $ and $\mathrm{F}$ evaluated at the point $leftch_(0), f_[0] ight) $. Let $f_CH \perp F}\leftch_{0}, F_CO} ight)$ be the conditional probability density function for variables $\mathrm{H} $ and $\mathrm{F}$ evaluated at the point $\leftch_003. f_{0} ight)$. Let $f_H \mid F}\leftch_[0], F_C0} ight $ be the conditional probability density function for random variables $\mathrm{H} $ given $\mathrm{F}$ evaluated at the point $\leftch_{0), f_C0} ight) $. Evaluate the following functions: \begin{tabular) (1/1 a. $f_CH, F) (20,0)=$ & (round to two decimals) | b. $f_CH \mid F) 20,0)=$ & (round to two decimals) C. SECH \mid F==$ & Cround to two decimals) W d. $ECH \mid F=1}=$ & Cround to two decimals) \end{tabular e. Use your answers to question c. and $0$. above to estimate the values of the following Conditional Expectation Function: $ECH \mid F 1=\beta_C0}+\beta_{1} F$ $\beta_{0}=$ $\beta_{1}=$ f. The share of women in the population, $E[F]=$ f. The share of women in the population, SE[F]=$ g. Use the law of iterated expectations, and your answers to e. and $\mathrm{f}$., to find the unconditional expectation of hours worked: $ECHT=E[ECH \mid F]=$ SP.SD.050