Question: Let be the circle , be the circle , be the circle , and be the circle . Define and . Define as wraps around

Let be the circle 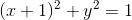Let be the circle , be the circle , be the circle 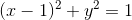, be the circle 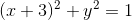, and be the circle 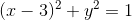. Define and . Define as 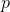wraps , be the circle around twice and wraps around twice, and are mapped homeomorphically onto and , and be the circle respectively. a) Give a presentation for and . Carefully, write down the .

Define and . Define as generators. where means the fundamental group of relative to the base point wraps around twice and wraps around twice, and are mapped homeomorphically onto and respectively.

a) Give a presentation for and . Carefully, write down the generators.

where means the fundamental group of 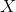. b) Compute as a subgroup of . where the map is relative to the base point .

b) Compute as a subgroup of .

where the map is the homomorphism induced by and defined by .

NOTE: The notations and definition can be found in textbook "Topology - Second edition by James Munkres"

Transcribed image text

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

An instanton is a quantum mechanical excitation that is localized in space like a particle. They are closely related to solitary waves or solitons that were first observed in the mid-nineteenth...

March 24", 2015 began like a typical morning at Zappos. Employees streamed into the online retailer's headquarters in Las Vegas, shuffling by the popcorn stand in the lobby, the makeshift bowling...

You are not limited in the number of pages you must use, but keep the following points in mind: 1) do not quote the authors of the text or the case unless it is necessary to make a point; 2) use...

Python: ** As discussed above at Where to split the loop, the basic loop logic works whether the poly.undraw() call is at the beginning or end of the loop. Write a variation makePoly2.py that makes...

PLEASE GUIDE ONLY NUMBER #2'S PROCEDURE PLEASE! :) THANK YOU VERY MUCH IN ADVANCE! You are a police officer trying to crack a case. You want to check whether an important file is in the evidence...

I am trying to answer this question. Any help is appreciated! (2) Let B, be the circle (r + 1)? + 1? = 1, A, be the circle (r - 1)3 + 1? = 1, An be the circle (x + 3)2 + 1? = 1 and Bo be the circle...

Describing Data Once we have collected data from surveys or experiments, we need to summarize and present the data in a way that will be meaningful to the reader. We will begin with graphical...

MATHEMATICIANS RISE TO A CHALLENGE ne of the theorems we teach in eighth grade is a + b= *, where c is the length of the hypotenuse of a right triangle in Euclidean space, and a and b are the lengths...

The new line character is utilized solely as the last person in each message. On association with the server, a client can possibly (I) question the situation with a client by sending the client's...

Analyze the Measurements Here is the lab video link where the data was collected (https://youtu.be/ydPXXJt-Lt0) The Physics behind the Measurement Analyze the Measurements The Physics behind the...

Duck Airlines charges all passengers the same $400 fare on one of its routes. The average flight carries 60 people in a plane with a capacity of 100. One third of the flyers are business travelers...

The deflection of a beam, y(x), satisfies the differential equation 24 dx4 w(x) on 0

The most common reason firms have unused fixed - asset capacity is that fixed assets Question 4 options: 1 ) are tax deductible. 2 ) can't be purchased on credit. 3 ) are subject to depreciation. 4 )...

CT Corp Comprehensive Question Canadian Tire Corporation, Limited ( Canadian Tire ) is a family of companies that includes a retail segment and a financial services division, among others. The retail...

7. View https://www.youtube.com/watch?v=mIkNzhM2b70 (Across the World with the Singapore Girl) and http://youtu.be/P5sGKR6NJBw (Singapore Airlines SQ Girl), and discuss how these videos might be...

1. Describe what is so special about SIAs five elements of its successful HR practices?

4. Why do you think are US full-service airlines largely undifferentiated lowquality providers? What are the reasons that none of the full-service airlines positioned itself and delivers as a high...