Question: Let be the class of computably enumerable sets. Prove the following: a) is closed under union and intersection b) contains all the finite sets and

Let Let be the class of computably enumerable sets. Prove the following: a) be the class of computably enumerable sets. Prove the following:

a) is closed under union and intersection b) contains all the finite sets is closed under union and intersection

b) and cofinite sets of natural numbers. c) If 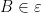and 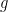is a total contains all the finite sets and cofinite sets of natural numbers.

c) If computable function then 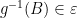. and . and 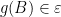image text in transcribed is a total computable function then image text in transcribed . and image text in transcribed.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Q:

2. Let be the class of computably enumerable (ce.) sets. Prove the following: (a) & is closed under union and intersection (b) & contains all the finite sets and cofinite sets of natural numbers. (c)...

Q:

Convex geometry 0.1 Dehn-Sommerville relations In this section we will talk about convex polytopes. One possible denition of a convex polytope uses the notion of a half-space: A closed half-space in...

Q:

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

Q:

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Q:

Let r and s be solutions to the quadratic equation x 2 b x + c = 0. For n N, define d0 = 0 d1 = r s dn = b dn1 c dn2 (n 2) Prove that dn = r n s n for all n N. [4 marks] (b) Recall that a commutative...

Q:

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Q:

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

Q:

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Q:

ret Electricity consumers are supplied with electricity from an electricity generating station. Electricity is distributed from the station to the various consumers through a network of transformers...

Q:

Estimate the number of bits needed to Huffman encode a random permutation of As, Bs and Cs, with each letter occurring one million times. [3 marks] (c) Estimate the number of bits needed to Huffman...

Q:

A frozen food company that makes burritos currently has employees making burritos by hand. They are considering purchasing equipment to automate the process and want to determine if the automated...

Q:

If a matrix is sensitive to roundoff errors, the computed value of its determinant may differ drastically from the exact value. For an example of this, set U = round(l00 * rand(l0)); U = triu((U, 1)...

Q:

water balance and cell functions are upset when theres an imbalance of which two minerals

Q:

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

Q:

___ 6. I will feel successful in my career only if I have a feeling of having made a real contribution to the welfare of society.

Q:

3. How does this fit with your preferences, career anchors, and values?

Q:

2. What potential barriers would you encourage Samuel to avoid?