Question: Let B(n) represent the number of binary search trees containing items 1, 2, 3, , n, then B(n) satisfies the following recurrence relation, B( 0)

Let B(n) represent the number of binary search trees containing items 1, 2, 3, , n, then B(n) satisfies the following recurrence relation, B( 0) = 1,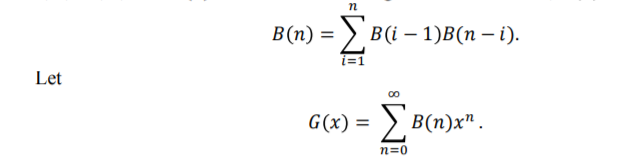Let B(n) represent the number of binary search trees containing items 1,

Verify via explicit power series manipulations that

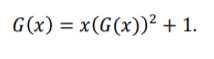
2, 3, , n, then B(n) satisfies the following recurrence relation, B(

n B(n) = (1 1)( - i). Let 00 G(x) = (n);". =0 G(x) = x(G(x))2 + 1. n B(n) = (1 1)( - i). Let 00 G(x) = (n);". =0 G(x) = x(G(x))2 + 1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Q:

The Barking Lot is a dog day care center. Design a flowchart or pseudocode for following: a. A program that accepts data for an ID number of a dogs owner, and the name, breed, age, and weight of the...

Q:

using a dynamic programming algorithm to solve this Let B(n) be the number of different binary search trees containing the n keys 1, 2,n. For this problem you will develop a dynamic programming...

Q:

[25 pts] We wish to search for a value v in a sorted array A of length n. (a) (10 pts] If we let T(n) denote the worst-case number of comparisons required for a basic balanced binary search, then...

Q:

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Q:

"Fortran, Algol and Lisp invented most programming language concepts 50 years ago; adding the concept of object-orientation suffices to explain all programming languages to date". To what extent is...

Q:

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Q:

Give the typing rules for Peano natural numbers and their eliminator.(ii) Using the rules given above, define the addition function.] (iii) Let a binary tree be either a leaf Leaf or a node...

Q:

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Q:

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

Q:

You have been asked to work as a usability consultant, for a company where the development team has created a new version of an existing product. Two important requirements were that the new user...

Q:

DETAILS What is the maximum segment length of a 100Base-FX netdwork, The last character ('X', etc) refers to the line code method used. Line code is a patdtern of voltage, current or photons used to...

Q:

A steel cable 1.25 in. in diameter and 50-ft long is to lift a 20-ton load. What is the length of the cable during lifting? The modulus of elasticity of the steel is 30 106 psi?

Q:

Air is expanded from 2000 kPa and 500C to 100 kPa and 50C. Assuming constant specific heats, determine the change in the specific entropy of air.

Q:

After reading the articles at Forbes http://www.forbes .com/sites/billconerly/2015/05/11/add-financial -modeling-to-your-operational-planning/ and http://...

Q:

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

Q:

6. Go to www.eldercare.gov, the Eldercare Locator, a public service of the U.S. Administration on Aging. What resources are available on this Web site? What topics do these resources cover?

Q:

3. Are certain kinds or types of jobs better for job sharing? Do the characteristics of the job, the manager, or the employees sharing the job have the most important influence on the effectiveness...

Q:

1. From a careers perspective, why would two employees decide to job share?