Let By showing (a) through (d), prove Let Rp+1 be an arbitrary unbiased estimate . By showing (a) through (c), prove CramerRaos inequality

Let

By showing (a) through (d), prove

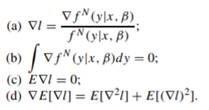
Let β˜ ∈ Rp+1 be an arbitrary unbiased estimate β. By showing (a) through (c), prove Cramer–Rao’s inequality

(a) E[(β˜ − β)(∇l)T ] = I .

(b) The covariance matrix of the vector combining β˜−β and ∇l of size 2(p+1)

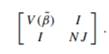
(c) Both sides of

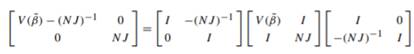
are nonnegative definite.

n (ylx, B) := [1 f(ylx. B).