Let c, R > 0 and suppose that , : R R are smooth functions such that (x) = (x) = 0 whenever

Let c, R > 0 and suppose that φ, ψ : R → R are smooth functions such that φ(x) = ψ(x) = 0 whenever |x| ≥ R. Let u(x, t) be the solution of

u_tt − c^2u_xx = 0, u(x, 0) = φ(x), u_t(x, 0) = ψ(x),

where x∈R and t≥0. Show that there exists some t_0 >0 such that

 

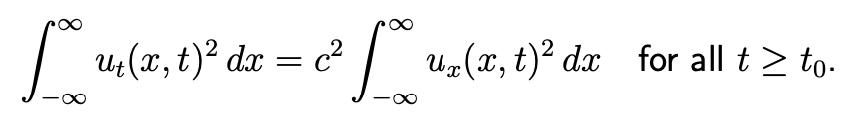
2 10 4 [ 14 (x, t) dx = c u(x, uz(x, t) dx for all t to.