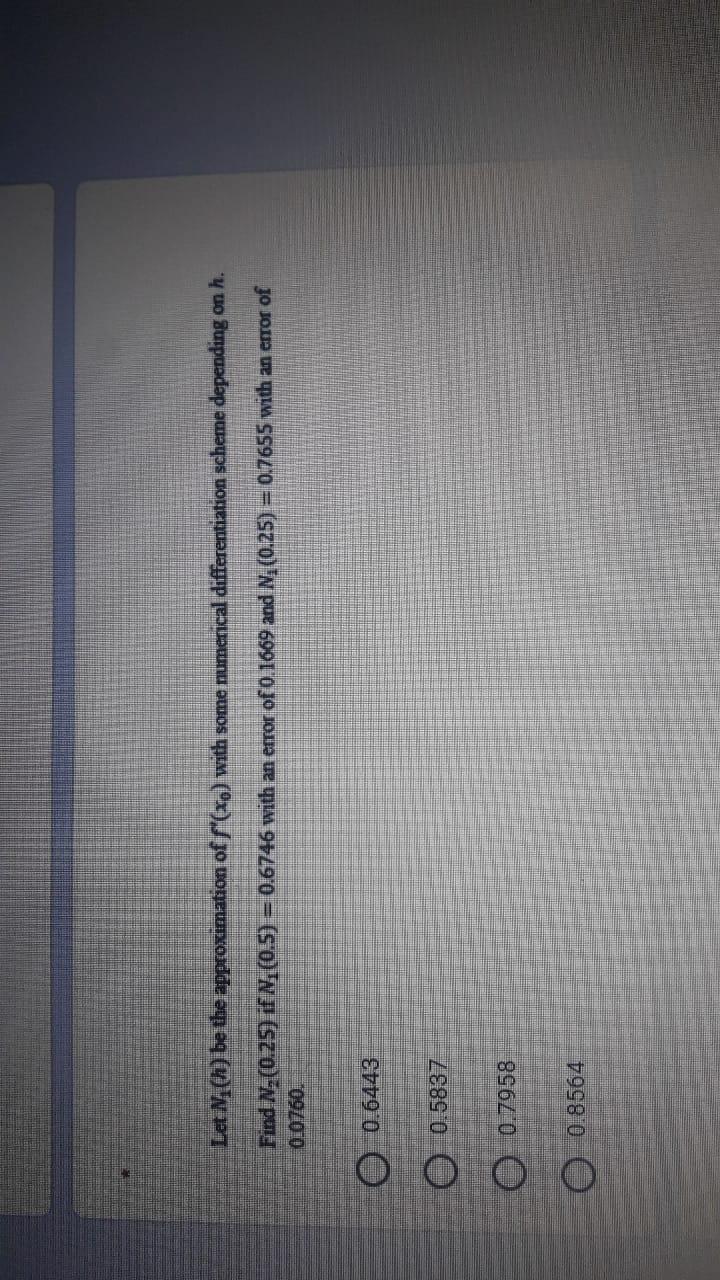
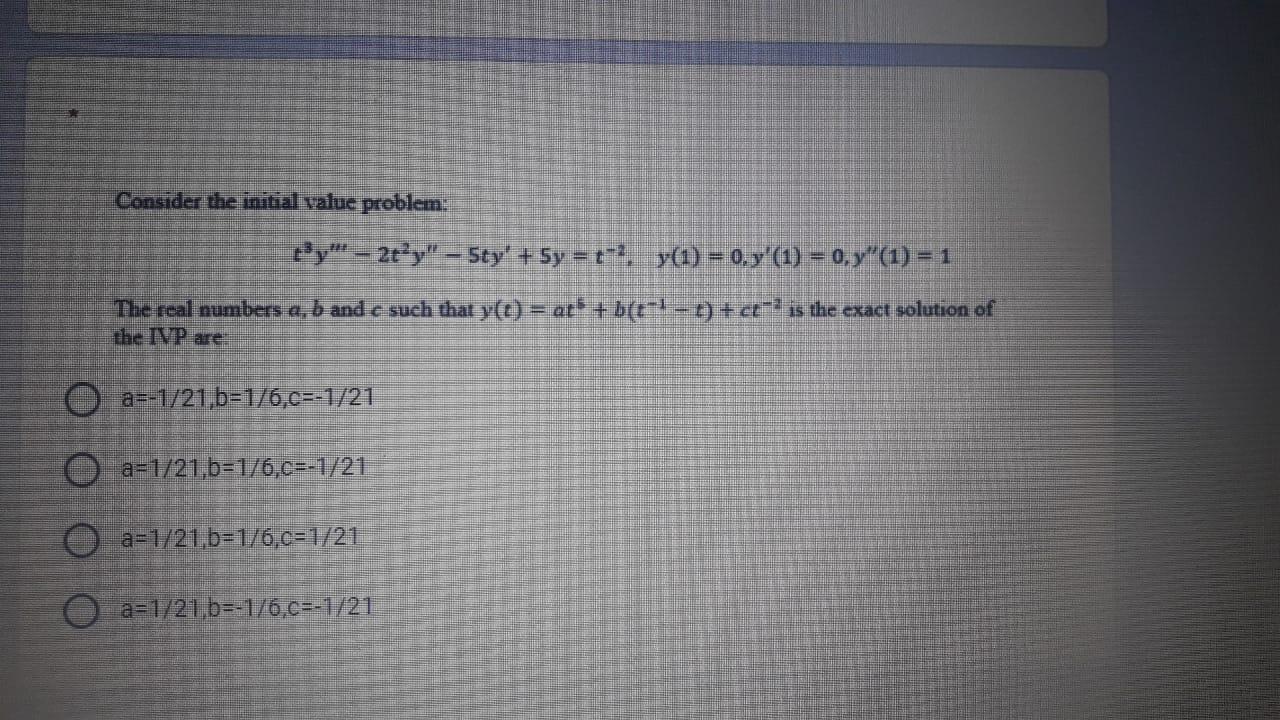
Let f be a smooth function on [1, 2]. Suppose that the following quadrature formula: f(x)dx & af(1) + bf (2) + cf"(1) has the highest degree of precision, then the constants a, b and c are: O a=5/6, b=1/6, c=1/3 O a=1/2, b=1/2, C=-1/12 a=-1/2, b=3/2, C=-1/6 a=2/3, b=1/3, c=1/6 Let M.Ch) be the approximation of "(*o) with some numerical differentiation scheme depending on h. Find Ny(0.25) if N.(0.5) = 0.6746 with an error of o. 1669 and N.(0.25) = 0.7655 with an error of 0.0760. O 0.6443 O 0.5837 O 0.7958 0.8564 Consider the initial value problem: ty" - 2ty" - Sty' + 5y = t-. y(1) = 0.y' (1) = 0.y" (1) = 1 The real numbers a, b and e such that y(c)= a1 + b(e-1-1) + ct? is the exact solution of the IVP are O a--1/21,b=1/6,C=-1/21 a=1/21,b=1/6,C=-1/21 O O O O a=1/21,b=1/6,0=1/21 O a=1/21,b=-1/6,C=-1/21