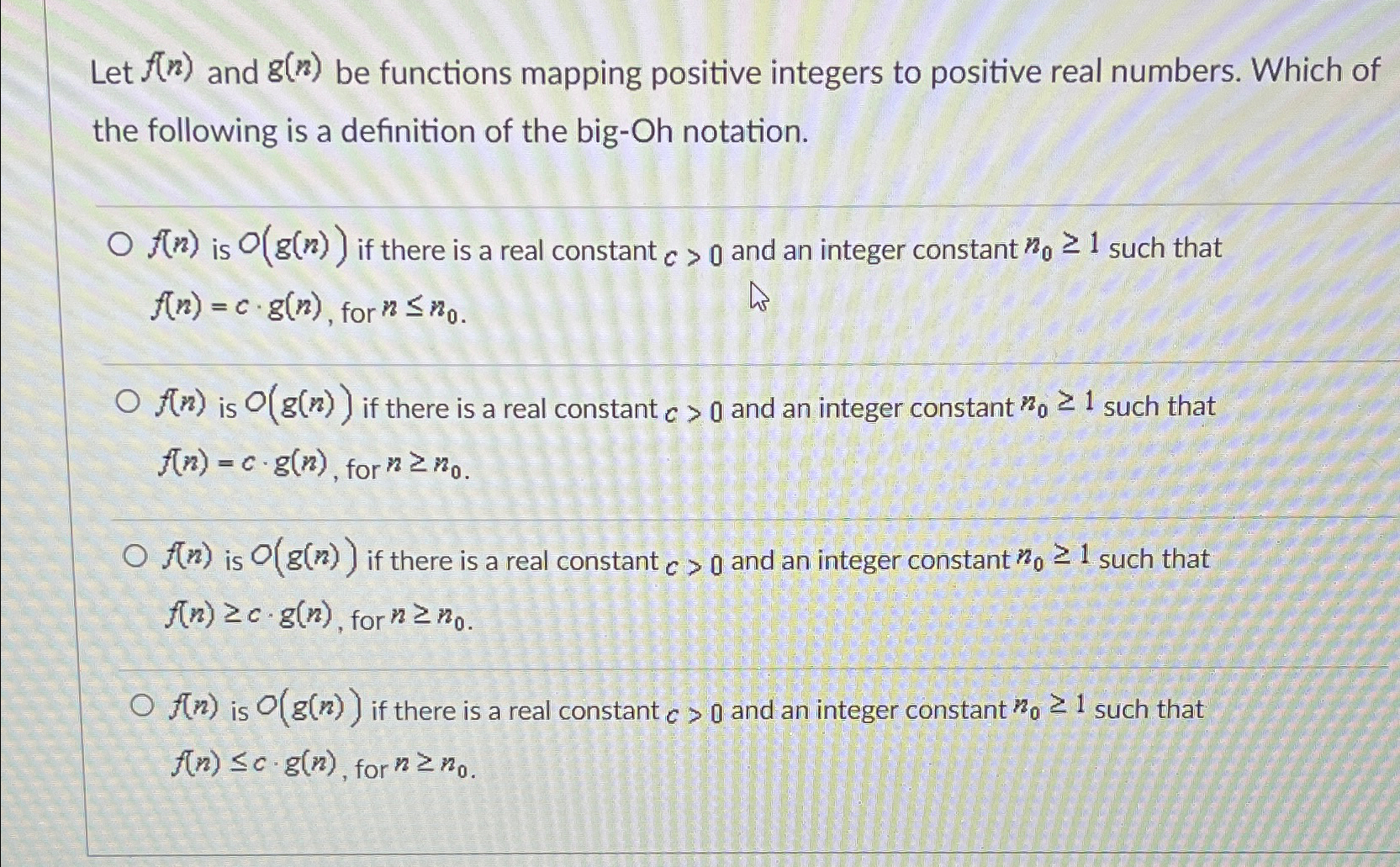
Question: Let f ( n ) and g ( n ) be functions mapping positive integers to positive real numbers. Which of the following is a
Let and be functions mapping positive integers to positive real numbers. Which of the following is a definition of the bigOh notation.
is if there is a real constant and an integer constant such that for
is if there is a real constant and an integer constant such that for
is if there is a real constant and an integer constant such that for
is if there is a real constant and an integer constant such that for
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


