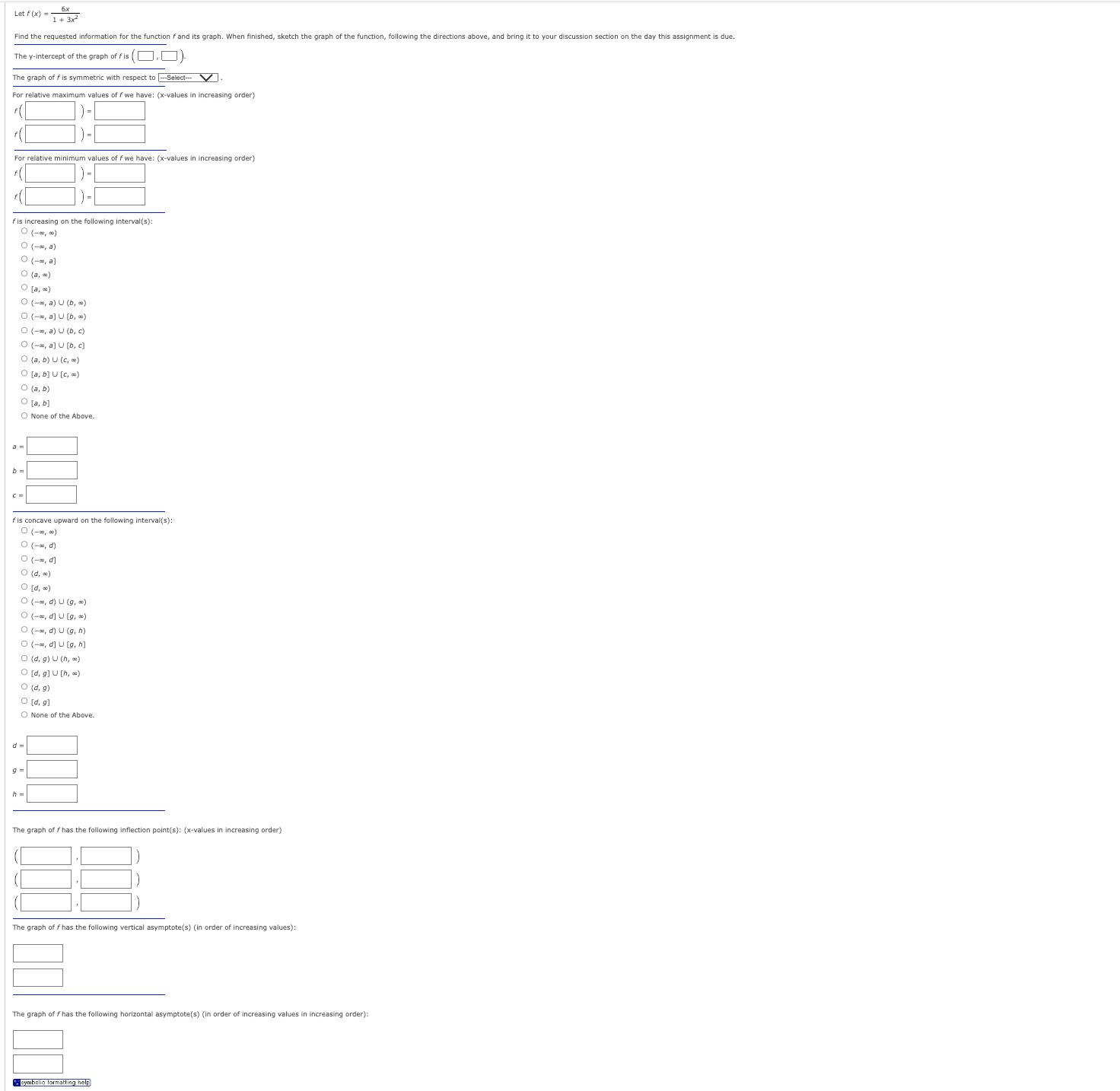
Let $f(x)=\frac{6x}{1+3x^2}$

The y$-$intercept of the graph of $f$ is $(,).$

The graph of $f$ is symmetric with respect to $--$ Select$--.$

For relative maximum values of $f$ we have: $(x-$values in increasing order$)$

$f()=$

$f(|,)=$

For relative minimum values of $f$ we have: $(x-$values in increasing order$)$

$t()=$

$f(,)=$

$f$ is increasing on the following interval$($s$)$:

$(-,)$

$(-,a)$

$O_{(-,a]}$

$0(a,)$

$[a,)$

$(-,a)(b,)$

$(-,a][b,)$

$(-,a)(b,c)$

$(-,a][b,c]$

$O(a,b)(c,)$

$[a,b][c,)$

$(a,b)$

$a,b$

None of the Above.

$b=$

$c=$

$f$ is concave upward on the following interval$($s$)$:

$0(-,)$

O $(-,d)$

$O_{(-,d]}$

$(d,)$

$0[d,)$

$(-,d)(g,)$

$(-,d][g,)$

$O(-,d)(g,h)$

$(-,d][g,h]$

$(d,g)(h,)$

$[d,g][h,)$

$($d$,$ g$)$

$[d,g]$

None of the Above.

The graph of $f$ has the following inflection point$($s$)$: $(x-$values in increasing order$)$

$(,,)$

$($

$,)$

The graph of $f$ has the following vertical asymptote$($s$)($in order of increasing values$)$:

The graph of $f$ has the following horizontal asymptote$($s$)($in order of increasing values in increasing order$)$: