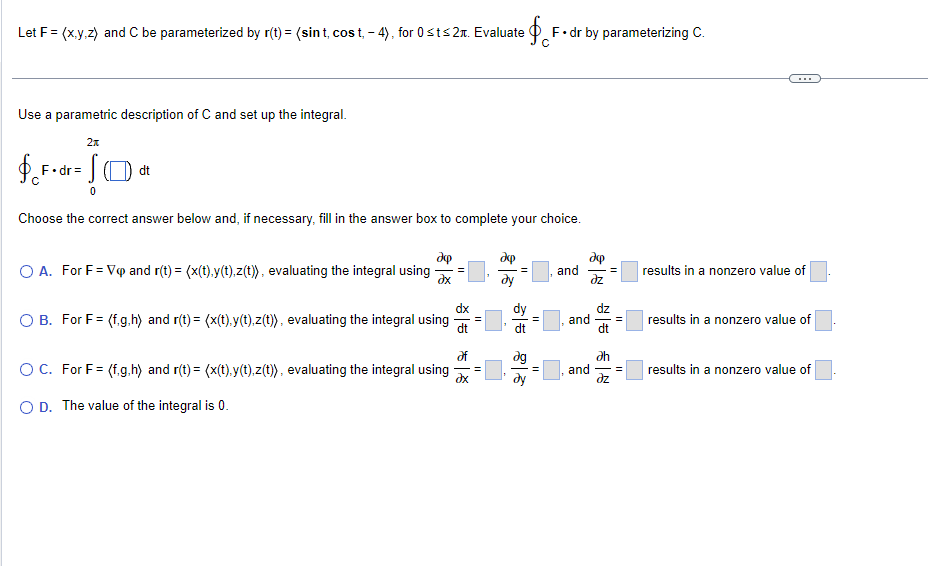
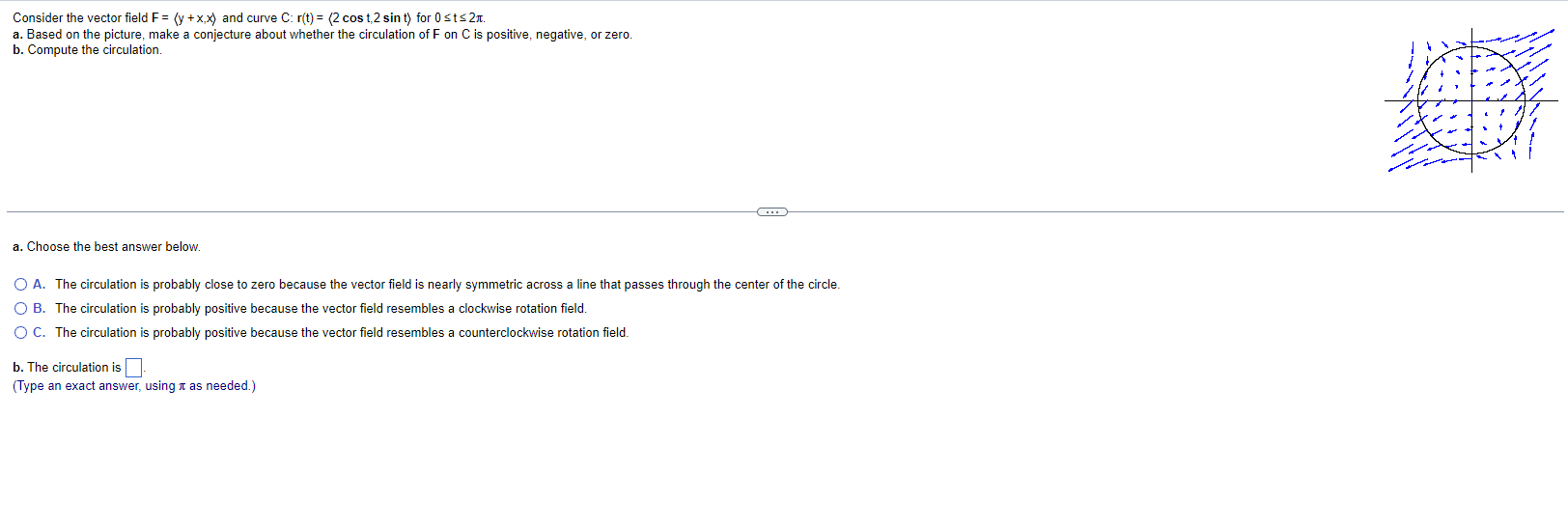
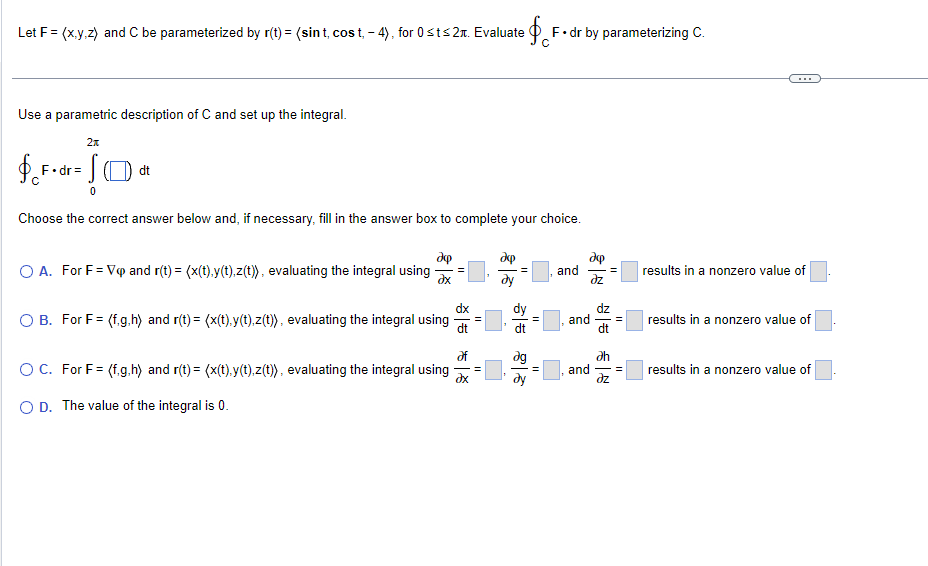
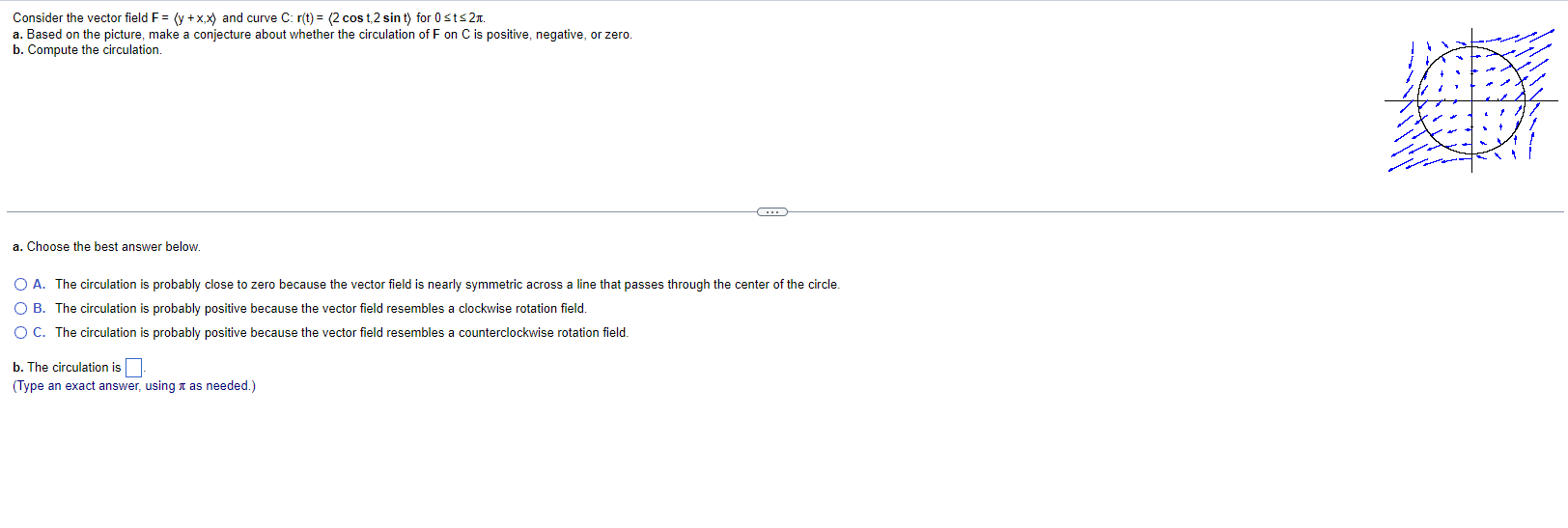
Let F= (x,y,z) and C be parameterized by r(t) = (sint, cost, - 4), for 0 sts 2x. Evaluate @ F . dr by parameterizing C. Use a parametric description of C and set up the integral. 2x $ F . dr = [ ( d 0 Choose the correct answer below and, if necessary, fill in the answer box to complete your choice. O A. For F= Vp and r(t) = (x(t),y(1),z(t)), evaluating the integral using - = and results in a nonzero value of dy dx dy az O B. For F = (f.g,h) and r(t) = (x(t),y(t),z(t), evaluating the integral using - dt and dt = results in a nonzero value of of dg oh O C. For F = (f.g,h) and r(t) = (x(t),y(1),z(t)), evaluating the integral using - = and = results in a nonzero value of O D. The value of the integral is 0.Consider the vector field F= (y + x,x) and curve C: r(t) = (2 cost,2 sint) for 0 sts 2x. a. Based on the picture, make a conjecture about whether the circulation of F on C is positive, negative, or zero. b. Compute the circulation. a. Choose the best answer below. O A. The circulation is probably close to zero because the vector field is nearly symmetric across a line that passes through the center of the circle. O B. The circulation is probably positive because the vector field resembles a clockwise rotation field. O C. The circulation is probably positive because the vector field resembles a counterclockwise rotation field. b. The circulation is (Type an exact answer, using It as needed.)