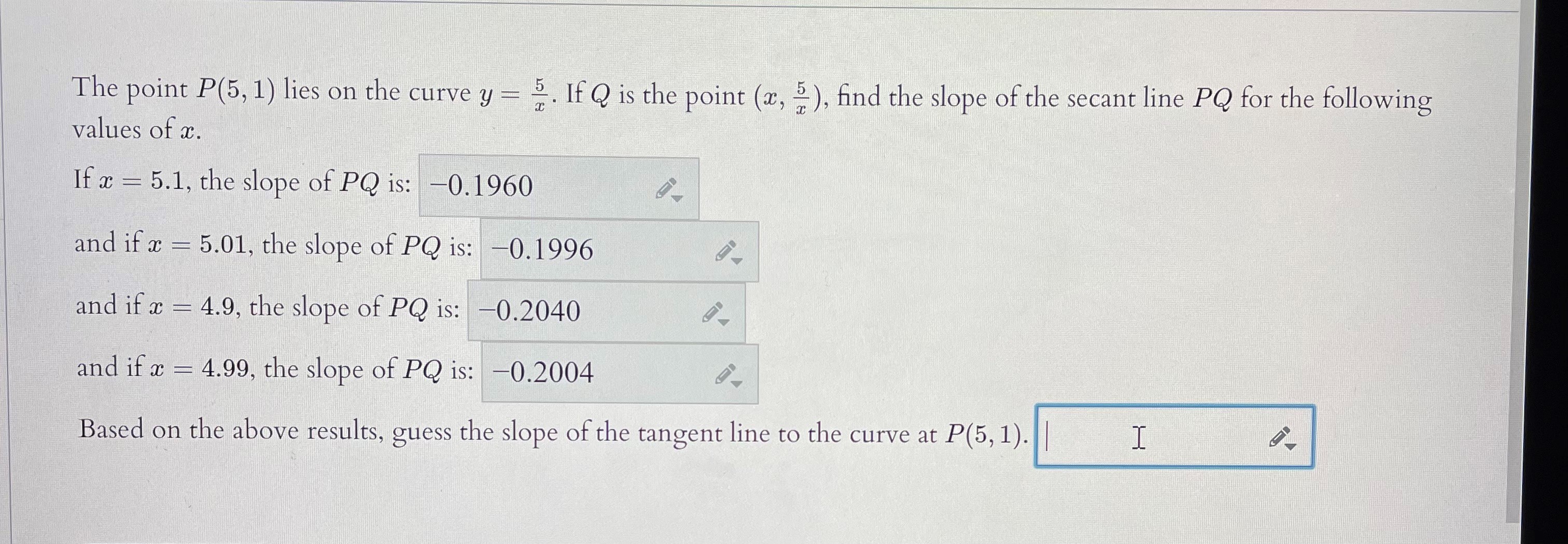
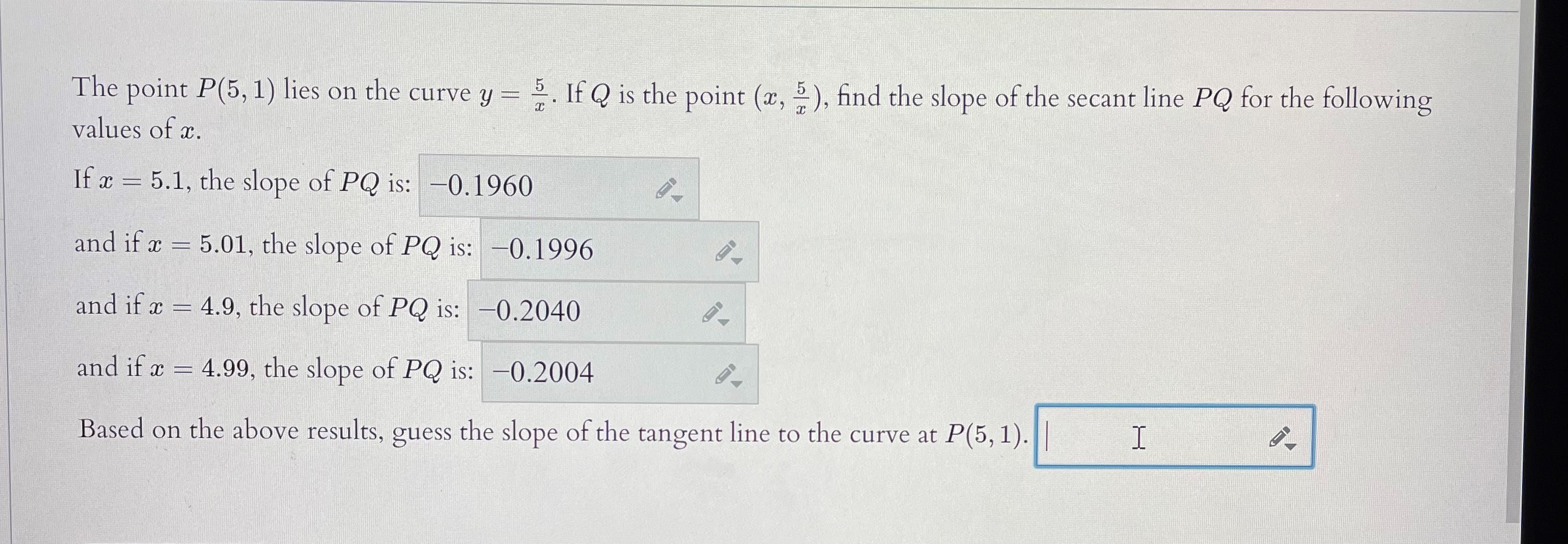
Let f(ac) = 3ac2 - 7ac + 5 The slope of the tangent line to the graph of f(a) at the point (4, 25) is The equation of the tangent line to the graph of f(x) at (4, 25) is y = ma + b for m and 6 : Hint: the slope is given by the derivative at x = 4, ie. lim f ( 4 + h) - f(4) hThe point P(16, 7) lies on the curve y = va + 3. Let Q be the point (x, Vx + 3). a.) Find the slope of the secant line PQ for the following values of x. (Answers here should be correct to at least 6 places after the decimal point.) If x = 16.1, the slope of PQ is: If x = 16.01, the slope of PQ is: If x = 15.9, the slope of PQ is: If x - 15.99, the slope of PQ is:Let f( ac ) = - a) Find the tangent line to the graph of the function at x = -3. y b) Find the normal line to the graph of the function at x = -3. y =The point P(5, 1) lies on the curve y = 2. If Q is the point (x, ), find the slope of the secant line PQ for the following values of x. If x = 5.1, the slope of PQ is: -0.1960 and if x = 5.01, the slope of PQ is: -0.1996 and if x = 4.9, the slope of PQ is: -0.2040 and if x - 4.99, the slope of PQ is: -0.2004 Based on the above results, guess the slope of the tangent line to the curve at P(5, 1)