Question: Let ( Fn) be a sequence defined by F1 = F2 = 1, Fn = Fn-1 + Fn-2 where n > 2. Prove by induction

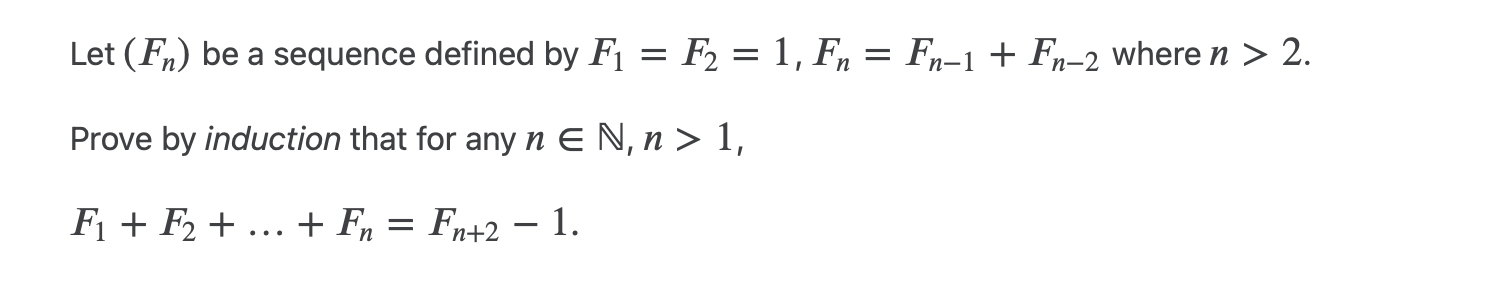
Let ( Fn) be a sequence defined by F1 = F2 = 1, Fn = Fn-1 + Fn-2 where n > 2. Prove by induction that for any n E N, n > 1, F1 + F2 + ... + Fn = Fn+2- 1.Use induction to show that for any natural n 2 3, one can be written as a sum of n distinct fractions of the form - where k is a k natural number. Example. For n = 3, 1 = + + 6 Hint. Note that + This is useful for the induction step. b +1 b(b + 1)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

4. (Induction/Recursion - 36 pt.) a. (5 pt.) Give a recursive definition of the sequence ana = n?, n=1,2,3,.. b. (13 pt.) Let fr be the nth Fibonacci number (fo = 0,f1 = 1, fn = fn-1 + fn-2 ). Prove...

4. (Induction/Recursion - 36 pt.) a. (5 pt.) Give a recursive definition of the sequence ana = n?, n=1,2,3,.. b. (13 pt.) Let fr be the nth Fibonacci number fo = 0,f1 = 1, fn = fn-1 + fn-2). Prove...

4. [10 points] The Fibonacci sequence is defined by fo = 0, f1 = 1, f2 = 1, fn = fn-1 + fn-2 (n>3). Its first few terms are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... Prove that for all n > 1:...

6. The Fibonacci sequence is defined by f1 = f2 = 1, and if n 2 3, then fn = fn-1+ fn-2. The first few terms are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. For all n 2 1, define an = fn (a) Prove that an = 1...

The Fibonacci sequence of numbers is defined as follows: The first and second numbers are both 1. After that, each number in the sequence is the sum of the two preceding numbers. Thus, the Fibonacci...

Consider Fibonacci number F(N), where N is a positive integer, defined as follows. F(1) = 1 F(2) = 1 F(N) = F(N-1) + F(N-2) for N > 2 a) Write a recursive function that computes Fibonacci number for...

7. (5 marks) Recall that the Fibonacci sequence { fn} is defined as follows: f1 = f2 = 1, and fn = fn-2+ fn-1, for n 2 3. Consider the sequence { n } given inductively by fn+1 $1 = 1, Sn for n > 1....

Prove this by bijection proof Recall that Fibonacci numbers are defined by F1 = F2 = 1 and recurrence relation Fn = Fn-1+ Fn-2 for n 2 3. Prove that Fn is the number of ways to tile a 2 x (n - 1)...

Fibonacci sequence is defined by F = 1, F2 = 1, F, = Fn-1 + Fn-2 for all n = 3,4,5, ... Using Complete Mathematical Induction prove that V5 1+ V5 V5 1 Fn 2

In the next production cycle there are 2,400 hours of machine press time available, 6,000 hours of fabrication, 3,300 hours of assembly, and 1,500 hours of testing capacity. Assume Gourmet Grill can...

The inverse Laplace transform of F(s) = 2s2+42s2+4 is

straight line depreciation on office equipment is variable, fixed, step, mixed?

The forfeited shares account is used to make up any shortfall: O to the forfeiting shareholder. the forfeited share reserve. on the issue of the shares. on the cash at bank account. Different...