Let f(t) and g(t) be functions moving in three-dimensional space.

f,g: R -> R^3

f,g are normal function

for fj(t),gj(t) ? R it can be written as (See SS1 (attachment))

If f1, f2, f3 is differentiable, it is written as (See SS2 (attachment))

When fj and gj are differentiable, show that (See SS3 (attachment))

The question means that show that the product rule can be derived from matrix

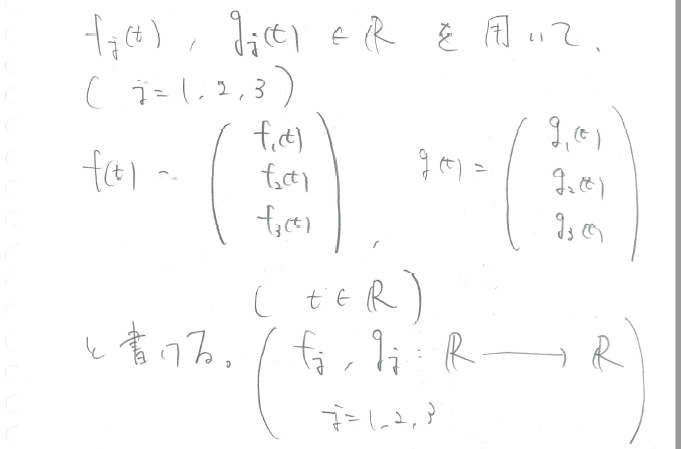
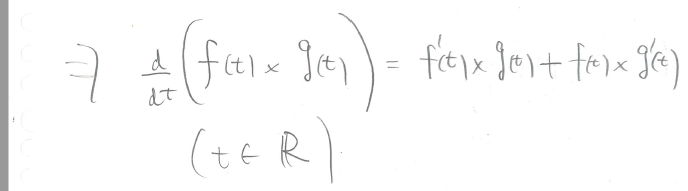
\f\f\f