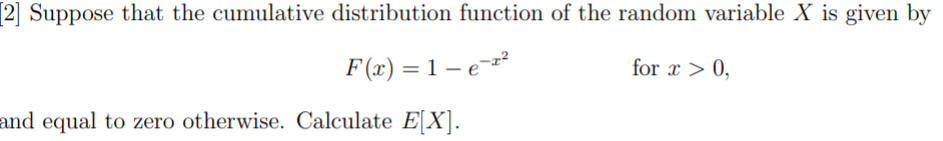
Let f(x, y) be the joint probability density function of X and Y, G be the probability distri- bution function of X/Y, and g be the probability density function of X/Y. We have that [1/2 0 < x < 1, 0 < y < 2 f(x, y) = 0 otherwise. Clearly, P(X/Y t) = 0 ift < 0. For 0 < t < 1/2, For t 1/2, P(X 1) = f ( S { dx ) dy = 1. P ( = 1) = [ ' ( S dy ) d x = 1-1/4- x/t 4t (Draw appropriate figures to verify the limits of these integrals.) Therefore, This gives 0 t