Let

f:x->Y

be a function, let

A

and

B

be subsets of

x

, and let

C

and

D

be cubsets of

Y

. Prove that\ (a)

f(A\\\\cup B)-f(A)\\\\cup f(B)

\ (b)

f(A\\\\cap B)subf(A)\\\\cap f(B)

\ (c)

f^(-1)(C\\\\cup D)=f^(-1)(C)\\\\cup f^(-1)(D)

\ (d)

f^(-1)(C\\\\cap D)=f^(-1)(C)\\\\cap f^(-1)(D)

\ (e)

f^(-1)(f(A))supA

\ (D)

f(f^(-1)(C))subC

.

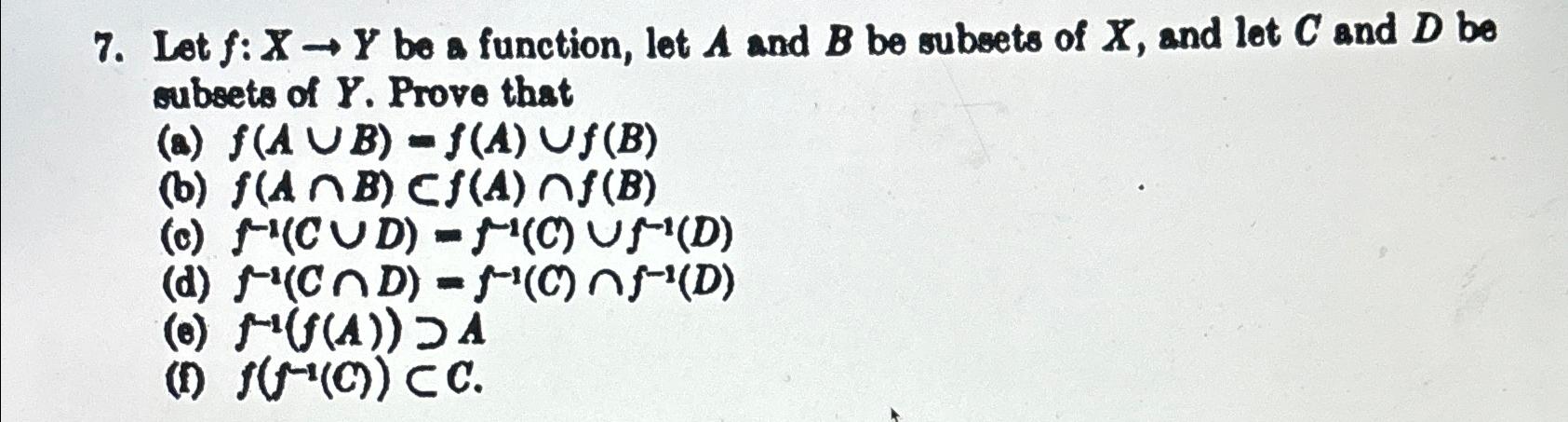
7. Let f:XY be a function, let A and B be subsets of X, and let C and D be subsets of Y. Prove that (a) f(AB)=f(A)f(B) (b) f(AB)f(A)f(B) (c) f1(CD)=f1(C)f1(D) (d) f1(CD)=f1(C)f1(D) (e) f1(f(A))A (I) f(f1(C))C