Question: Let G be a non-Abelian group such that |G| < 15 with proper subgroups H and K such that G = H x K.

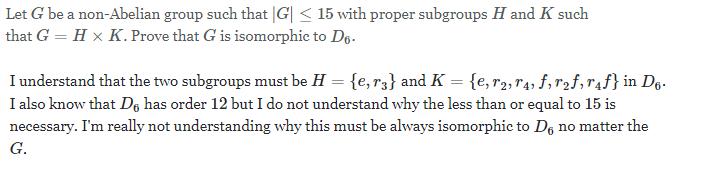
Let G be a non-Abelian group such that |G| < 15 with proper subgroups H and K such that G = H x K. Prove that G is isomorphic to Dg. I understand that the two subgroups must be H = {e,r3} and K = {e,r2,"4, f,r2f,raf} in Dg. I also know that Dg has order 12 but I do not understand why the less than or equal to 15 is necessary. I'm really not understanding why this must be always isomorphic to Do no matter the G.

Step by Step Solution

★★★★★

3.43 Rating (150 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Solm et G be a nonAbeliam group Such that with prop... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Fowlkes et al. (1988) reported results of a survey of employees of a large national corporation to determine how satisfaction depends on race, gender, age, and regional location. The data are at the...

Let G be a simple graph with n vertices. Show that a) G is a tree if and only if it is connected and has n - 1 edges. b) G is a tree if and only if G has no simple circuits and has n 1 edges.

Let G be a directed graph on n vertices. If the associated undirected graph for G is Kn, prove that vV[od(v)]2 = vV [id(v)]2.

Let G be a loop-free undirected graph on n vertices. If G has 56 edges and has 80 edges, what is n?

What is the solution to the following system? 4+=3 28+4=9 520+7=19 Let s and t be dummy variables such that s and t go from 0 to positive infinity. The solution set is (4s + t + 4, s, 2t + 1, t). Let...

I need two ratios provided based on the financial statement of a company (fullfinancial attached). I need the price-earnings ratio (the formula of price per share divided by earnings per share) and...

CASE 13 Yeti in 2020: Can Brand Name and Innovation Keep it Ahead of the Competition? Diana R. Garza David L. Turnipseed University of the Incarnate Word University of South Alabama n early 2020,...

Help please. I need as much help as possible. In the excel file are all the questions. The first sheet has all the instructions. The sources are also attached. If I could have answers before...

Milestone 2 Assignment Section One In today's world, diversity, equity, and inclusion (DEI) in the workplace have become crucial for companies to flourish. DEI promotes a fair and just workplace and...

Explain it briefly 1. Let G be non-abelian group. Show that for all x E G, Z(G) o(Z(G)) + 1. 9. Let N be normal in G. Show that either cl(a) n N = q or cl(a) c N for all a EG. 10. Let N 0. Let N be...

Superstores like Costco and Sams Club serves as wholesalers to businesses but also target consumers who are willing to pay a fixed fee in order to get access to the lower wholesale prices offered in...

Name a quantum-mechanical system for which the spacing between adjacent bound-state energy levels (a) Remains constant as E increases; (b) Increases as E increases; (c) Decreases as E increases.

The balance sheet of the Hillcrest Home Care Service, a not-for-prot organization providing assistance to the elderly, is presented here: 1. As best as you can tell from the balance sheet, what are...

QUESTION 9 Find g ' ( x ) . , g ( x ) = e x x 2 - 1

If you were Lenny, to what degree would you consider the other stakeholders described in this scenario? If you were the president of a football team owned by shareholders in the same situation, to...

The City of Pfeiffer starts the year of 2015 with the general fund and an enterprise fund. The general fund has two activities: education and parks/recreation. For convenience, assume that the...

Snyder Computer Chips, Inc., is experiencing a period of rapid growth. Earnings and dividends are expected to grow at a rate of 15 percent during the next two years, at 13 percent in the third year,...

Design the HARDWARE INVENTORY LISTING Web page, showing the computers available in each room at each campus. The CAMPUS is selected from a drop-down list displaying the CAMPUS DESCRIPTION. When the...

Carnival Corporation has recently placed into service some of the largest cruise ships in the world. One of these ships, the Carnival Breeze, can hold up to 3,600 passengers, and it can cost $750...

Name of coil used in past to produce faradic current

Let H and K be subgroups of a group G. Define ~ on G by a ~ b if and only if a = hbk for some h H and some k K. a. Prove that ~ is an equivalence relation on G. b. Describe the elements in the...

Part (ii) or (ii)' of the Fundamental Theorem (2.5) is equivalent to: an intermediate field E is normal over K if and only if the corresponding subgroup E' is normal in G = Aut K F in which case G i...

Let H and K be subgroups of a group G, where e is the identity of G. Prove that if |H| = 10 and |K| = 21, then H K = {e}.

m = 12 (25p) 2. (In this question, if the last digit of your student ID is even, then n is 10 more than the last digit of your student ID. For instance, if your ID is 17025062, then m = 12. If the...

Question Number: 11 Correct: 1 Wrong: 0 Let G be a non-abelian group of order 125. Then the total number of elements in Z(G) = {xeGgx=xg for all g = G} equals Question Number: 12 Correct: 1 Wrong: 0...

= 7. Let |G| = 56. Follow the steps below to construct a full list of distinct nonabelian groups of order 56 (ten of them). = (a) Show that G has either a normal Sylow 2-subgroup S or a normal Sylow...