Let G = (V, E) be a directed graph. A black hole is a vertex v ? V such that

all vertices u 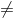v have an outgoing edge (u, v) leading to v

and v has no outgoing edge.

(a) Prove or disprove: in a directed graph, there is at most one black hole.

(b) Design an algorithm which can detect whether or not there is a black hole in a directed graph. Your score on this question will depend on how efficient your algorithm is. You must describe your algorithm in plain English (no pseudocode). You must clearly state what graph representation you are working with (adjacency matrix or adjacency lists). You must give the running time of your algorithm and explain why you get this running time. Maximum one page.