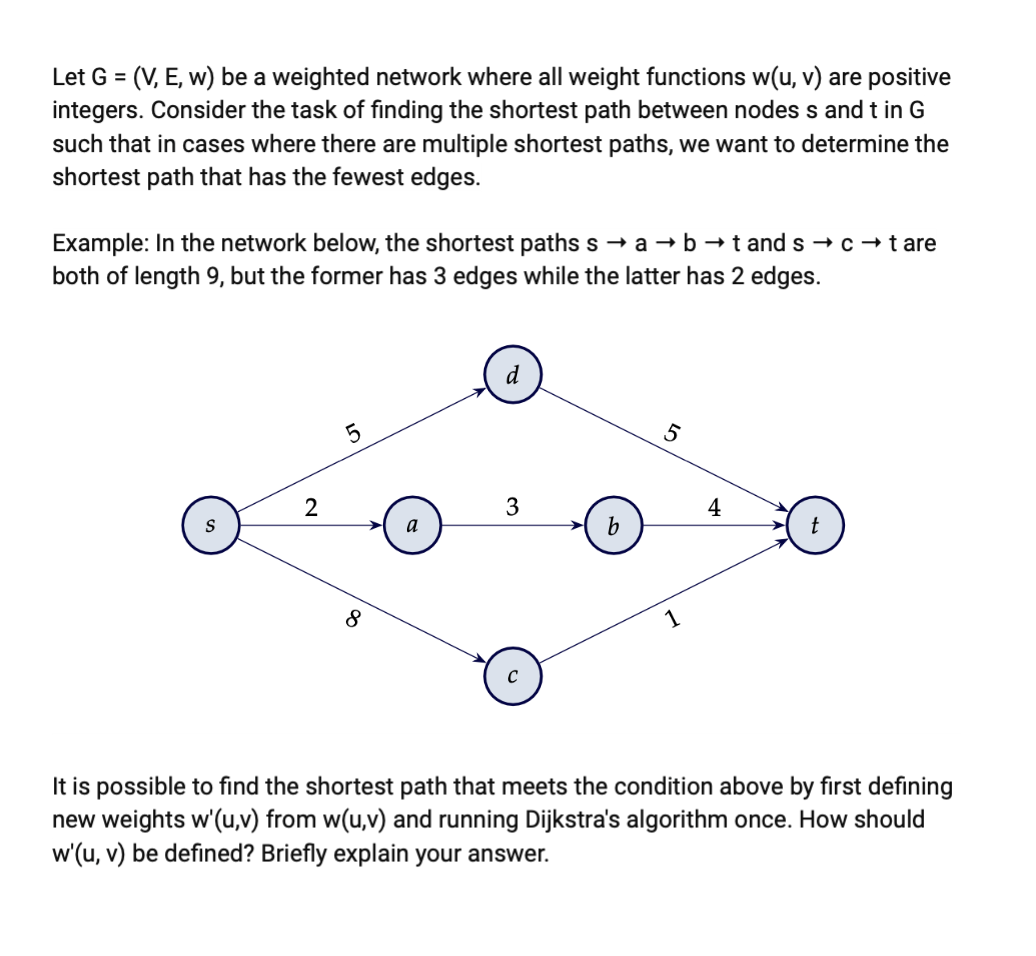
Let $G=(V,E,w)$ be a weighted network where all weight functions $w(u,v)$ are positive integers. Consider the task of finding the shortest path between nodes $s$ and $t$ in $G$ such that in cases where there are multiple shortest paths, we want to determine the shortest path that has the fewest edges.

Example: In the network below, the shortest paths $sabt$ and $sct$ are both of length $9,$ but the former has $3$ edges while the latter has $2$ edges.

It is possible to find the shortest path that meets the condition above by first defining new weights $w^{\text{'}}(u,v)$ from $w(u,v)$ and running Dijkstra's algorithm once. How should $w^{\text{'}}(u,v)$ be defined? Briefly explain your answer.