Question: Let $G_{i}$ be a group with a normal subgroup $H_{i} unlhd G_{i}$ for $i=1, 2$. Show that (a) $H_{1} times H_{2} unlhd G_{1} times G_{2}$.

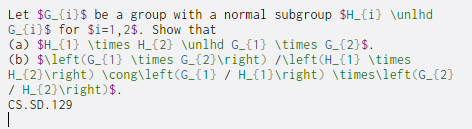
$Let $G_{i}$ be a group with a normal subgroup $H_{i} \unlhd$

Let $G_{i}$ be a group with a normal subgroup $H_{i} \unlhd G_{i}$ for $i=1, 2$. Show that (a) $H_{1} \times H_{2} \unlhd G_{1} \times G_{2}$. (b) $\left(G_{1} \times G_{2} ight) Aleft(H_{1} \times H_{2} ight) \cong\left(G_{1} / H_{1} ight) \times\left(G_{2} / H_{2} ight) $. CS. SD. 129

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Number Theory (2) (5 points) Let G be a group. In class we defined a subgroup of G to be a nonempty subset H satisfying: . For any h, h' E H, we also have hh' E H. . For any h EH, hale H. Show that a...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Module 6: Enable Others to Act Page 99 Describe the responsibility you think a leader has for respecting and valuing everyone in the group. How is that different from liking everyone in the group?...

Math 3310 - Algebraic Structures I 12/12/11 Final Ir Give precise denitions 4 of the following 7. (5 points each) 1 2 3 4 5 6 7 II. Work 3 of the following 5 problems. Determine if the statement is...

Explain ments of nite order does it have? 20. Suppose that G is an Abelian group of order 35 and every element of G satises the equation x35 = e. Prove that G is cyclic. Does your argument work if 35...

Fact If all) and b|a, then a = b or a = b. Division Algorithm For any a.b E Z with b > 0. there exist unique q E Z (quotient) and 7' E Z (remainder) such that a : bq + 7' with 0 S 7" 1 is prime if...

11. Write out the cycle decomposition of the eight permutations in $4 corresponding to the elements of Dg given by the action of Dg on the vertices of a square (where the vertices of the square are...

Please Solve This Question 1. If f : G - G' is a homomorphism then show that f (G) = (f (a) | a E G} is a subgroup of G'. We also write f(G) = Imf (Image f). Show further that if H is normal in G...

April 2011 WEATH3021 Group Theory Midterm test QUESTION 1 (a) Let G be a group and / be a subgroup of G. Define what is meant by a Normal subgroup of G and give one equivalent statement (3) (b) Let H...

.... 39. 40. 41. 42. 43. 45. 46. (1995 Putnam Competition) Let S be a set of real numbers that is closed under multiplication. Let T and U be disjoint subsets of S whose union is S. Given that the...

The average starting salary of students who graduated from colleges of Business in 2009 was $48,400. A sample of 100 graduates of 2010 showed an average starting salary of $50,000. Assume the...

Consolidation workpaper entries are made to eliminate 100 percent of the unrealized profit from the land account in downstream sales of land. Is 100 percent also eliminated for upstream sales of land?

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

=+10. Suppose the United States adopted central planning for its economy, and you became the chief planner. Among the millions of decisions that you need to make for next year are how many

=+ 9. Your roommate is a better cook than you are, but you can clean more quickly than your roommate can. If your roommate did all the cooking

=+ b. How does the reduction in benefits associated with higher earnings affect peoples incentive to work past age 65?