Question: Let g(z) and h(x) be partially computable functions. Show that there is a partially computable function f(x) such that f(x) for precisely those values

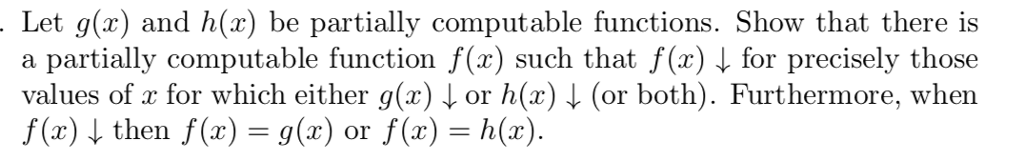
Let g(z) and h(x) be partially computable functions. Show that there

Let g(z) and h(x) be partially computable functions. Show that there is a partially computable function f(x) such that f(x) \ for precisely those values of x for which either g(x) or h(2) (or both). Furthermore, when f(x) then f(x) g(x) or f(x) = h(x). Let g(z) and h(x) be partially computable functions. Show that there is a partially computable function f(x) such that f(x) \ for precisely those values of x for which either g(x) or h(2) (or both). Furthermore, when f(x) then f(x) g(x) or f(x) = h(x)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

MATLAB ASSIGN 1- Follow Directions and Complete. Will Thumbs Up! Directions: Unless otherwise specified, your write-up should contain the MATLAB input commands, the corresponding output, and the...

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

1. Evaluate the following limits if they exist. 3x2 - 6x + 8 (a lim x-70 2 - 4x + 7 (Do not use L'Hospitals Rule) Answer: 3 (b) lim 2 2 - 8x + 12 2-2 202 - 3x + 2 (Do not use L'Hospitals Rule)...

Please use C++ for this program. Please read the problem and follow the instruction in main.cpp for this program. Problem: - Design an abstract class called Shape: - Private variables double x and...

1) Find the range of these functions. Give your answer as a simple/short sentence using plain English. The following solution to (a): S = {2x | x Z} despite being correct, will receive 0 points....

(Recall that Z = {2, 1, 0, 1, 2, . . .} is the integers, R the real numbers, (0,) the positive reals, and [0,) the non-negative reals.) Let f : [0, ) [0,); f(x) = x [ x/2] Let g : Z Z; g(x) = 2x + 3...

13-20 are just T and F answers needed 10. What is the value for (2)? 2 (a) 3 (b) 9 (c) 4+9 + 16 (d) 2+ 3+4 (e) None of the above. For the next two questions let g : A B and f : B C where A-B =...

Need solution for Ex 3 pg 87 of Second Edition :Computability, Complexity, and Languages Fundamentals of Theoretical Computer Science Martin D. Davis,Ron Sigal,Elaine J. Weyuker Let us call a...

Divide into two groups, and prepare arguments for and against the following behavior: Im a regular customer of a mens clothing mail-order company, and it sends me new catalogs about six times a year....

Emeka Company has provided the following information: $50 Sales price per unit Variable cost per unit 14 Fixed costs per month $18,000 Calculate the contribution margin per unit. A. $36 B. $14 OC....

4. A pyramid with a triangular base has a volume of 50 cm. If the base and the height of the triangular base are 5 cm and 8 cm respectively, find the height of the pyramid.

P-1) (100 Pts.) A chemical manufacturing company (CMC) has a contract for the procurement of the neccssaly chemicals from four suppliers. The chemicals purchased from Supplier A are priced at $20...

Are you repelled by touches from strangers? What about touches from people who are not your age (children or the elderly)? What about being touched by a colleague or a professorsomeone you have a...

A Does the piercing even matter? What type of message does the tongue stud send?

Have you ever taken an online or distance-learning course? Were you happy with the instruction and the amount of interaction? It is challenging to both present and respond nonverbally in courses...