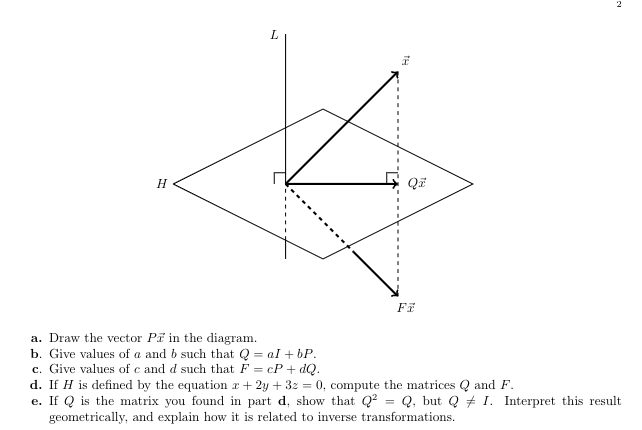
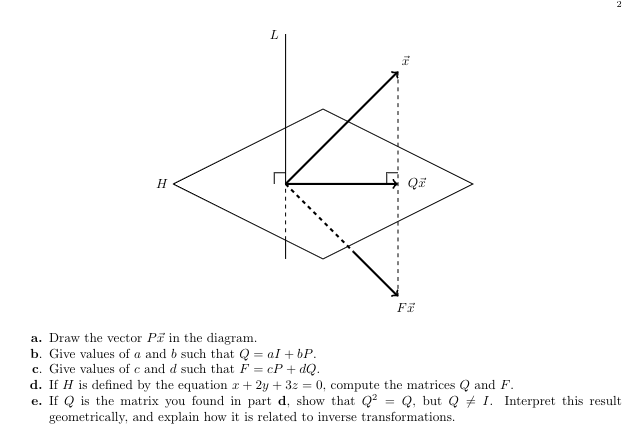
Let H be a plane through the origin in Ro, and let L be the line through the origin which is perpendicular to H. Consider the following matrices: P = the 3 x 3 matrix which projects vectors orthogonally onto L. Q = the 3 x 3 matrix which projects vectors orthogonally onto H. F = the 3 x 3 matrix which reflects vectors orthogonally across H. The transformations defined by Q and F are illustrated by the following diagram: 12 L HI H a. Draw the vector Pr in the diagram. b. Give values of a and b such that Q = al + bP. c. Give values of c and d such that F = cP + dQ. d. If H is defined by the equation + + 2y + 32 = 0, compute the matrices Q and F. e. If Q is the matrix you found in part d, show that Q' = Q, but Q # /. Interpret this result geometrically, and explain how it is related to inverse transformations