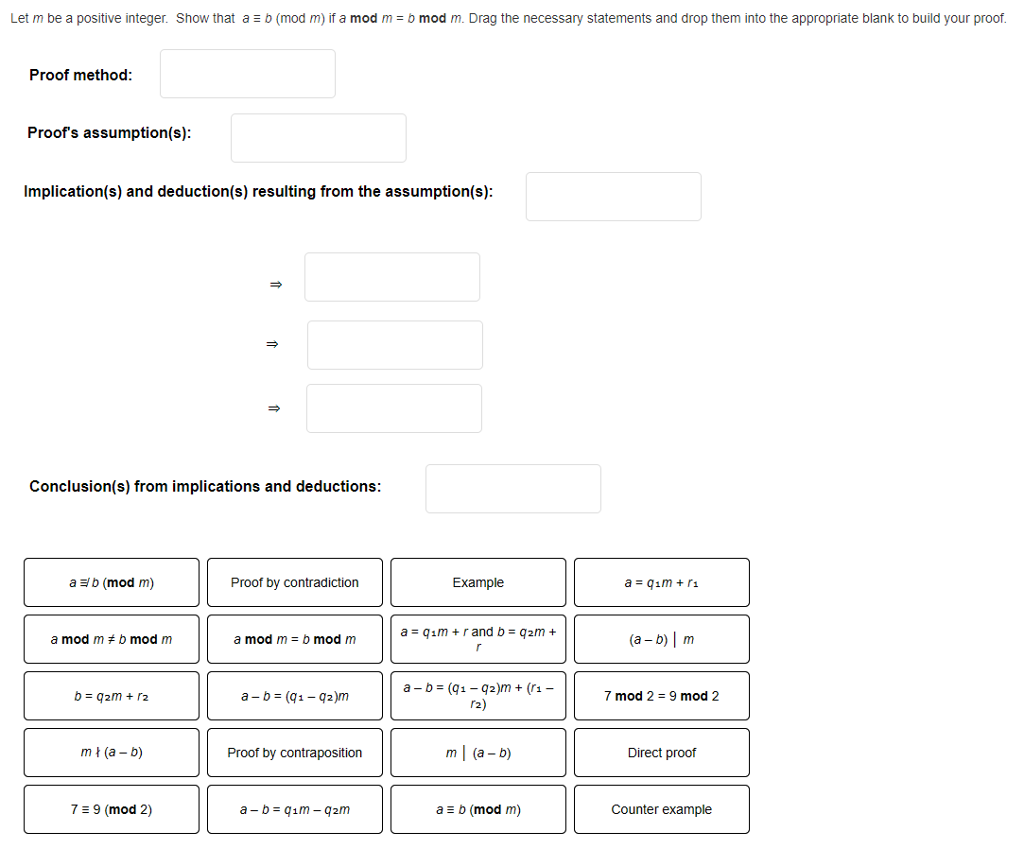
Let m be a positive integer. Show that a b mod m if a mod m = b mod m Drag the necessary statements and drop them into the appropriate blank to build your proof Proof method: Proofs assumption(s) Implication(s) and deduction(s) resulting from the assumption(s): Conclusion(s) from implications and deductions a b (mod m) Proof by contradiction Example a=q|m + r and b-q2/m + amod m b mod m amod m = b mod m (a-b) | m -D- (-)(7 mod 2-9 mod2 mt (a-b) Proof by contraposition m (a -b) Direct proof 7 9 (mod 2) ab (mod m) Counter example