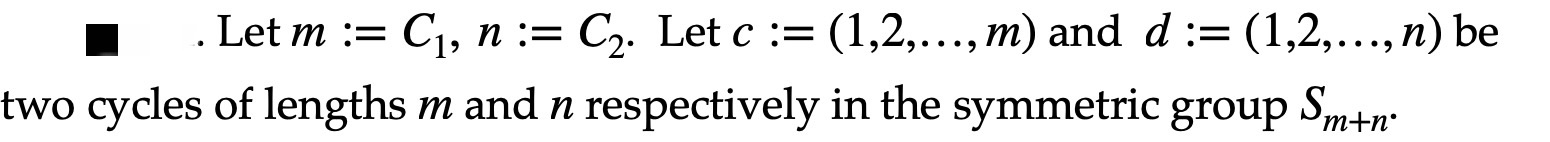
Let m := C1, n:= C2. Let c := (1,2,..., m) and d:= (1,2,..., n) be two cycles of lengths m and n respectively in the symmetric group Sm+n. D2 a. How many non-isomorphic abelian groups of order CC2 are there? b. List them. c. Elements of order 2 in a group are called transpositions. Are there transpositions in each of the abelian groups of order CC2? (It is not necessary to list them all if they exist: it is better to provide some short reason or maybe a few examples.) Let m := C1, n:= C2. Let c := (1,2,..., m) and d:= (1,2,..., n) be two cycles of lengths m and n respectively in the symmetric group Sm+n. D2 a. How many non-isomorphic abelian groups of order CC2 are there? b. List them. c. Elements of order 2 in a group are called transpositions. Are there transpositions in each of the abelian groups of order CC2? (It is not necessary to list them all if they exist: it is better to provide some short reason or maybe a few examples.)