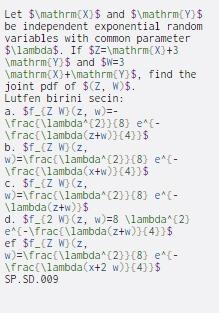
Let $\mathrm{X}$ and $\mathrm{Y}$ be independent exponential random variables with common parameter $\lambda$. If $2=\mathrm{X}+3 \mathrm{Y}$ and $w=3 \mathrm{X}+\mathrm{Y} $, find the } joint pdf of $CZ, W$. Lutfen birini secin: a. $f_(Z W) (z, W=- \frac{\lambda^{2}}{8} ec- \frac{\lambda(z+w) }{4}}$ b. $f_CZ W (z, w=\frac{\lambda^{2}}{8} ^{- ent \frac{\lambda (x+w)}{4}}$ c. $f_{Z W (z, \\2]] w)=\frac{\lambda 2] } [8] - ent- \lambda (z+w)}$ d. $F_{2 W (z, w)=8 \lambda (2) e^{-\frac{\lambda(z+w)}{4}}$ ef $f_CZ W CZ, w=\frac{\lambda^{2}}{B} ^{- ent- \frac{\lambda (x+2 w) }{4}}$ SP. SD.009