Question: Let n be a positive integer. The trace of an (n x n)-n1atrix A z: [am] is the sum of its diagonal entries: . tr(A)

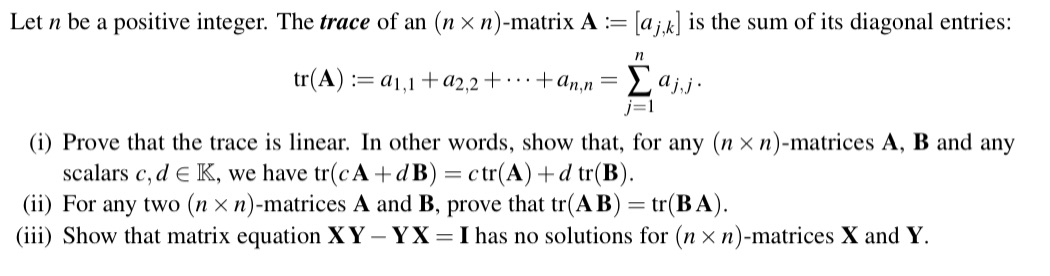
Let n be a positive integer. The trace of an (n x n)-n1atrix A z: [am] is the sum of its diagonal entries: . tr(A) := a1,1+02.2 + ' ' +3\"!!! = Z \"is? j=l (i) Prove that the trace is linear. In other words, show that, for any (n X n)-matrices A, B and any scalars c,d E K, we have tr(cA +dB) = ctr(A) +d tr(B). (ii) For any two (n x n)-matrices A and B, prove that tr(AB) = tr(B A). (iii) Show that matrix equation XY YX = I has no solutions for (n x n)-rnatrices X and Y

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

NWAC Electronics manufactures four types of simple cables for a defense contractor. Each cable must go through four sequential operations: splicing, soldering, sleeving, and inspection. The following...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Please use C++ for this program. Please read the problem and follow the instruction in main.cpp for this program. Problem: - Design an abstract class called Shape: - Private variables double x and...

This assignment asks you to write bash shell scripts to compute matrix operations. The purpose is to get you familiar with the Unix shell, shell programming, Unix utilities, standard input, output,...

A researcher measured the number of tree species per 0.1 hectare plot along the Black, Huron, and Vermilion rivers. The data are summarized in the table below: Here is a partial ANOVA table...

The pGreen plasmid that we are using in lab this week has a gene called amp". What is the purpose of this gene for our experiment? A. It will make cells that have taken up the plasmid glow green when...

Wilson and company has accounts payable of 15,000, long term debt of 35,000, common stock with a value of 75,000, sales in the amount of 100,000, cash in the amount of 25,000 and accounts receivable...

A company issues 1,050 shares of its common stock for $33,600 cash. Prepare journal entries to record this event under each of the following separate situations.