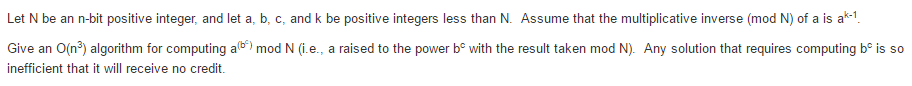
Let N be an n-bit positive integer, and let a, b. c. and k be positive integers less than N. Assume that the multiplicative inverse (mod N) of a is a^k-1. Give an 0(n^3) algorithm for computing a^(bc) mod N (i.e.. a raised to the power b^c with the result taken mod N). Any solution that requires computing b^c is so inefficient that it will receive no credit. Let N be an n-bit positive integer, and let a, b. c. and k be positive integers less than N. Assume that the multiplicative inverse (mod N) of a is a^k-1. Give an 0(n^3) algorithm for computing a^(bc) mod N (i.e.. a raised to the power b^c with the result taken mod N). Any solution that requires computing b^c is so inefficient that it will receive no credit