Question: Let N(t) be a Poisson process with parameter A and X (t) is defined as follows: 1=0 X (t ) = -1) N (t) 130.(a)

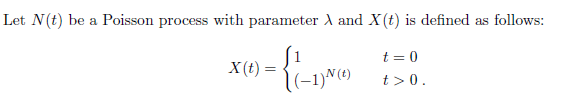
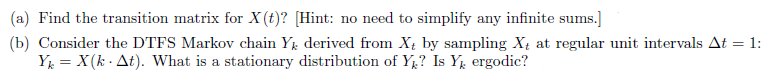
Let N(t) be a Poisson process with parameter A and X (t) is defined as follows: 1=0 X (t ) = -1) N

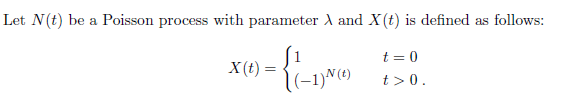
to simplify any infinite sums.] (b) Consider the DTFS Markov chain Yx

Let N(t) be a Poisson process with parameter A and X (t) is defined as follows: 1=0 X (t ) = -1) N (t) 130.(a) Find the transition matrix for X (t)? [Hint: no need to simplify any infinite sums.] (b) Consider the DTFS Markov chain Yx derived from Xt by sampling X at regular unit intervals At = 1: Yk = X(k . At). What is a stationary distribution of Y,? Is Y, ergodic

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

(a) How does the use of condition codes complicate the implementation of a superscalar processor that supports out-of-order execution? [4 marks] (b) A branch predictor with a high prediction accuracy...

Chapter 5 Discrete Markov process Suppose we have a sequence of random variables, {X0 , X1 , . . .} = {Xn } , which is also n=0 called a stochastic process. In this chapter, we study a commonly used...

Please help me find the answers Exercise 7.5.2: Evaluating compositions. Let Ti : R3 - R3, T2 : R' _ R3, and T3 : R -> R' be linear transformations defined as follows. 1+2 T1 2+3 T2 = 21 - $2 T3 2 C1...

Queuing theory question,thanks Exercise 3.1. Amy and Bill simultaneously write a bid on a piece of paper. The bid can only be either $2 or $3. A referee then looks at the bids, announces the amount...

solve attached Assuming that the population standard deviation is 60, how large a sample would be needed to provide a 95% confidence interval with a margin of error of 5? Question 19 options: 959 554...

Suppose that the random variable X has an exponential distribution with parameter ? > 0. (i) What are the probability density function, fX(x), and the probability distribution function, FX(x), for...

1. Which of the following statements is NOT true of investment trusts? A They are public companies. B They can raise both loan and equity capital. C They are open-ended investment vehicles. D Their...

Please help me to obtain clear solutions A portfolio of insurance policies contains two types of risk. Type I risks make up 80%% of claims and give rise to loss amounts which follow a normal...

MATH S350 TMA 01 Hints Question 1 Let A and B be the event that water is contaminated with excessive amount of pollutant A and pollutatnt B respectively. Remarks: 1. Half of those communities whose...

Jumpa EV Pte Ltd wants to embark on a vehicle equipment project. For this project, it needs to invest in some initial research and development but will reap handsome returns in the next three years....

16. What is the nth term of the arithmetic sequence 7, 9, 11, 13, 15, 17, ..? A. 3n+4 B. 4n+3 C. n+2 D. 2n+5 1 1 17. What is the nth term of the harmonic sequence ....? 2' 4' 6' 8 1 A. n+1 B. n +1 1...

Let f ( t ) = { ( 0 if t 3 ) , ( 4 ( t - 3 ) if 3 = t 6 ) , ( 1 2 if t > 6 ) : } Find the Laplace transform, F ( s ) of f ( t ) F ( s ) = \ sigma ^ ( 4 ) ( e ^ ( - 3 s ) ) / ( s ^ ( 2 ) ) - 4 ( e ^ (...

Consider the Weibull distribution f(x) = {β/δ(x/δ) β1 e (x/δ), 0 (a) Find the likelihood function based on a random sample of size n. Find the log likelihood. (b) Show...

In a physics laboratory experiment, a coil with 200 turns enclosing an area of 12 cm 2 is rotated in 0.040 s from a position where its plane is perpendicular to the earth's magnetic field to a...

Figure is an overhead view of a rigid rod that turns about a vertical axle until the identical rubber stoppers A and B arc forced against rigid walls at distances rA = 7.0 cm and rB = 4.0 cm from the...

In Figure a rectangular slab of slate rests on a bedrock surface inclined at angle = 26. The slab has length L = 43 m, thickness Z = 2.5 m, and width 17 = 12 m, and 1.0 cm3 of it has a mass of 3.2...

Figure represents an insect caught at the midpoint of a spider-web thread. The thread breaks under a stress of 8.20 x 108 N/m2 and a strain of 2.00. Initially, it was horizontal and had a length of...

Question 1: From the standpoint of an individual concerned with accounting controls, discuss and evaluate Johnson Toy Companys present policies for handling returned items. Question 2: Answer...

1. Provide new information that contains more than 59 items, depending on the recipients capacity.

3. Give away need to know information and you will get back information that you find useful.

4. Present multiple themes at once. Then you will get to know a little about how others think, when some of the themes are rejected.