Question: Let o be the surface 6x + 9y + 8z = 7 in the first octant, oriented upwards. Let C be the oriented boundary of

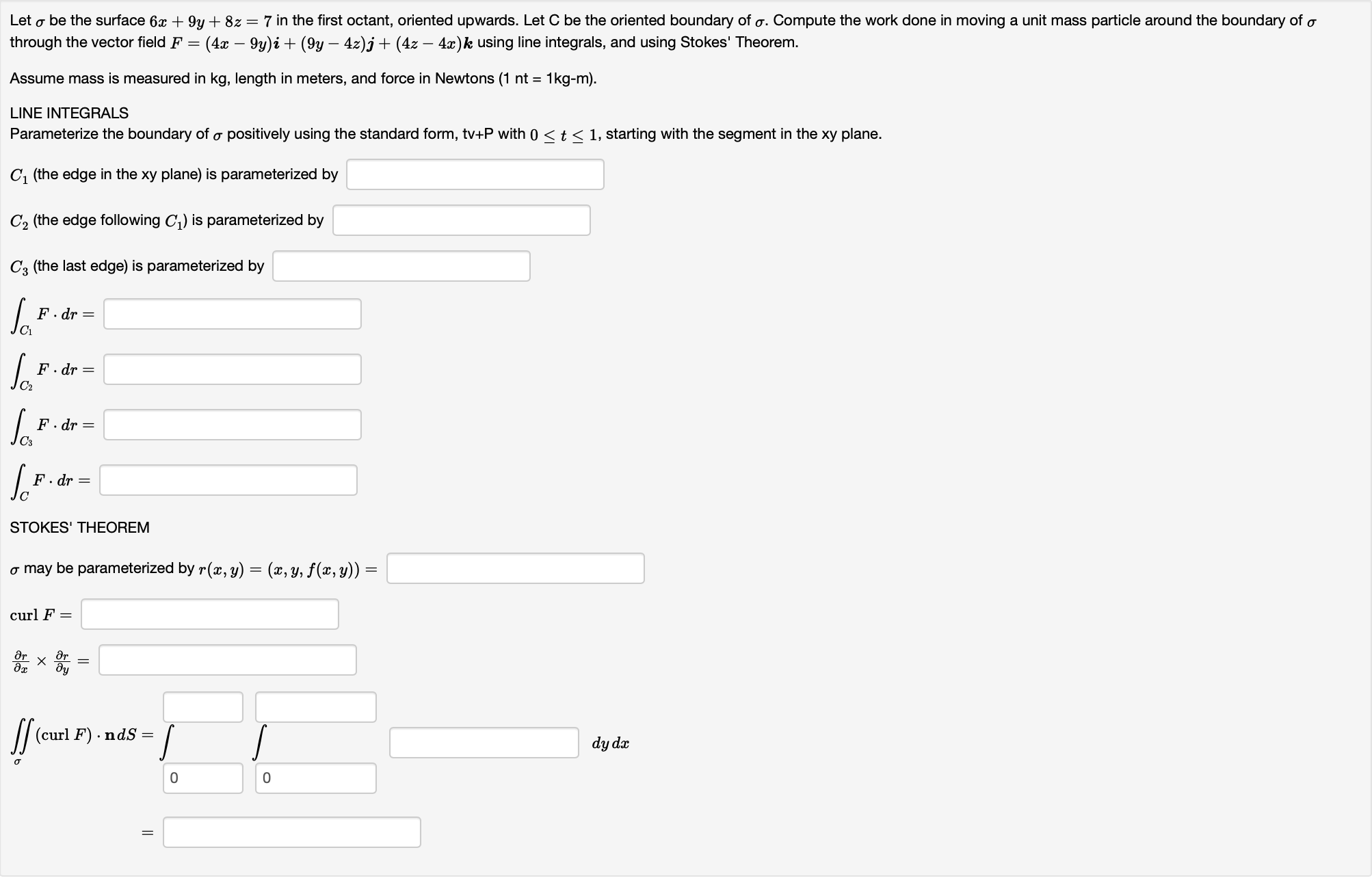
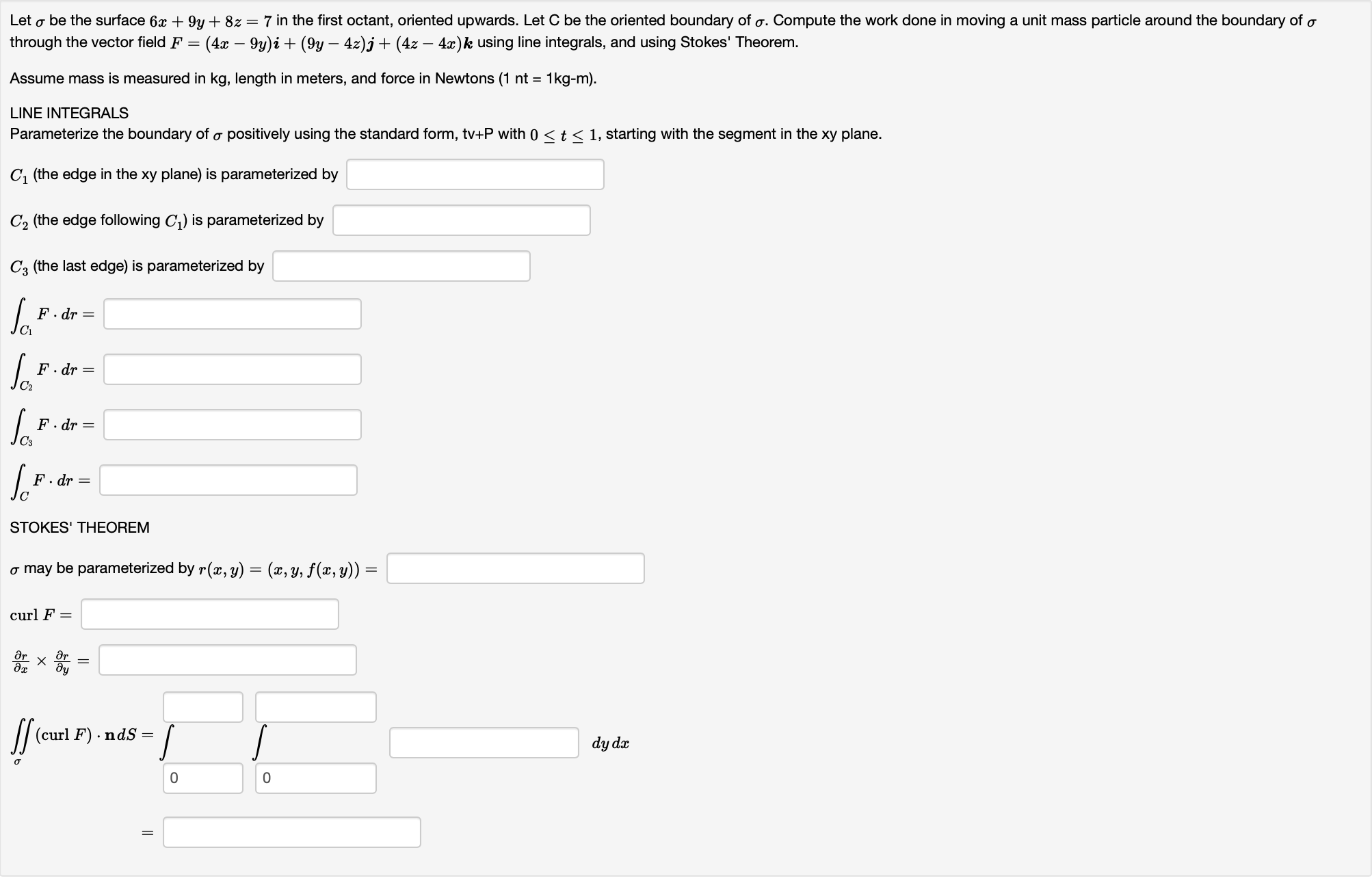
Let o be the surface 6x + 9y + 8z =

Let o be the surface 6x + 9y + 8z = 7 in the first octant, oriented upwards. Let C be the oriented boundary of o. Compute the work done in moving a unit mass particle around the boundary of o through the vector field F = (4x - 9y)i + (9y - 4z)j + (4z - 4x) k using line integrals, and using Stokes' Theorem. Assume mass is measured in kg, length in meters, and force in Newtons (1 nt = 1kg-m). LINE INTEGRALS Parameterize the boundary of o positively using the standard form, tv+P with 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let o be the surface 10x +7y +8z = 2 in the first octant, oriented upwards. Let C be the oriented boundary of o. Compute the work done in moving a unit mass particle around the boundary of o through...

(1 point) Let o be the surface 6x + 3y + 9z = 6 in the first octant, oriented upwards. Let C be the oriented boundary of 6. Compute the work done in moving a unit mass particle around the boundary of...

Let be the surface 10x+5y+6z=4 in the first octant, oriented upwards. Let C be the oriented boundary of . Compute the work done in moving a unit mass particle around the boundary of through the...

DUE TONIGHT I NEED HELP ASAP! Let be the surface 7 x 9 y 9 z = 2 in the first octant, oriented upwards. Let C be the orierted boundary of e . Compute the work done in moving a unit mass particle...

Let o be the surface which is the part of the graph of 10z + 7y + 5z = 10 in the first octant, oriented upwards. Let C' be the oriented boundary of . Compute the work done in moving a unit mass...

Let o be the surface which is the part of the graph of 10x + 7y + 5z = 10 in the first octant, oriented upwards. Let C be the oriented boundary of o. Compute the work done in moving a unit mass...

Please only answer ques 5-9 3:27 Reset Done 8. [7 marica] Use Stokes' theorem to compute the surface integral N - / (V xG) . ds for the voctor field G(z, y. 2) = (ever.x3=), where & is the half of...

MA 261 PRACTICE PROBLEMS 1. If the line ` has symmetric equations y x1 z+2 2 = 3 = 7 , nd a vector equation for the line `0 that contains the point (2; 1; 3) and is parallel to `. A. ~ = (1 + 2t)~...

Prepare appropriate reports that will support the evaluation of data in Phase 2. With additional data provided, you are to select reports that will help address the proprietor's concerns. Some...

Solve Problem 11 using the critical region method of testing. Compare your conclusions with the conclusion obtained by using the P-value method. Are they the same?

An insurance company has an automobile policy with a liability limit of $100,000. The probability that the company will incur a loss of at least $50,000 on any one policy is 0.05. Assume the...

Group Assignment ( Version 1 ) On February 1 0 , 2 0 2 5 , You, CPA, just met with a new client, Joe Junior. He was referred by one of your existing clients. During the online meeting, you have...

Write a program to print following triangle using nested for loop.

A. NZ IFRS 10 defines the parent-subsidiary relationship in terms of control rather than majority ownership. Write down one advantage and one disadvantage of control as the basis for...

The BarBQ Restaurant sells hot lunches and snacks to the crews of ships that dock at the port of Mobile. In order to have "exclusive rights" to this, the captains of the ships not only receive free...

Suppose a restaurant estimates its price elasticity of demand is -3.0 and its income elasticity is 2.0. It has been shut down but now is allowed to reopen at only 50% of its original level of...

Corpus Christi Corporation reported the following pretax (and taxable) information for 2010: Income from continuing operations........................$400,000 Loss on disposal of Segment...

Tori and some other childeen experimented with balls to see which ones rolled. First using a piece of cardboard to use as a ramp, they angled it on a block to the floor to test the balls. Then Tori...

Are you in favor of price gouging during natural disasters? Why or why not? : lop96

What is the opportunity cost of the economics profession? : lop96

In the chapter, we discussed how price ceilings can put goods in the wrong place, as when too little heating oil wound up in New Jersey during a harsh winter in the 1970s. Price controls can also put...