Let P₂ be the real vector space of polynomials in x of degree at most 2, and let T be the real vector space of upper triangular 2 2 matrices:{ ?[a0?bc?]? | a, b, c ? R }. The vector space P₂ is equipped with the inner product

= ???11?p(x)q(x)dx? , and the vector space T is equipped with the inner product=tr(A^tB), where tr denotes trace.

Let L:P₂ ->T be given by L(p(x)) := ?[p?(1)0??01?f(x)dxp(?1)?]? . Find L*(?[10?23?]? ).

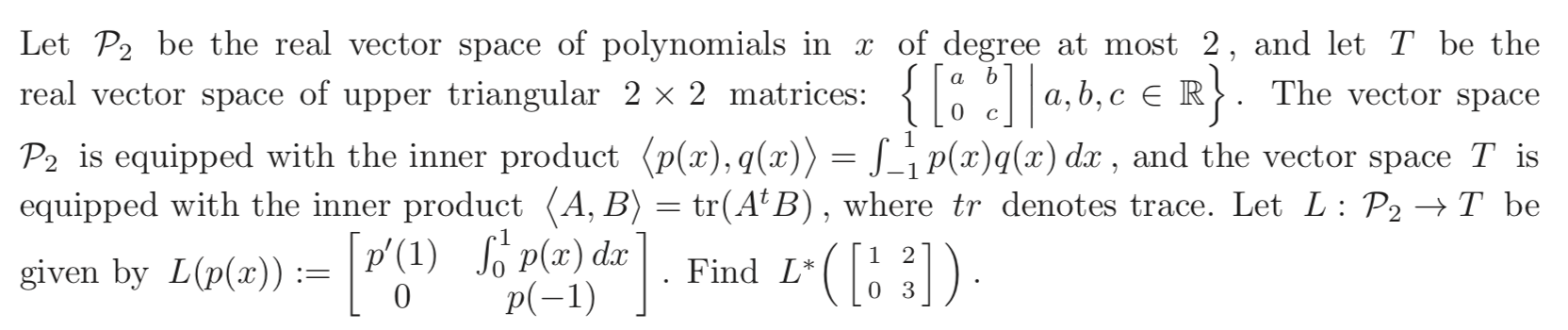
Let 732 be the real vector space of polynomials in a: of degree at most 2, and let T be the real vector space of upper triangular 2 x 2 matrices: { [3 1:] a,b,c E R} . The vector space 732 is equipped with the inner product (10(33), q(:c)) = f_11 p(:n)q(:r:) 03$ , and the vector space T is equipped with the inner product (A, B) = tr(AtB) , where tr denotes trace. Let L : 'Pg > T be given by L(p(:n)) := 10,31) fgpzzgvfm] . Find L*( [g g] )