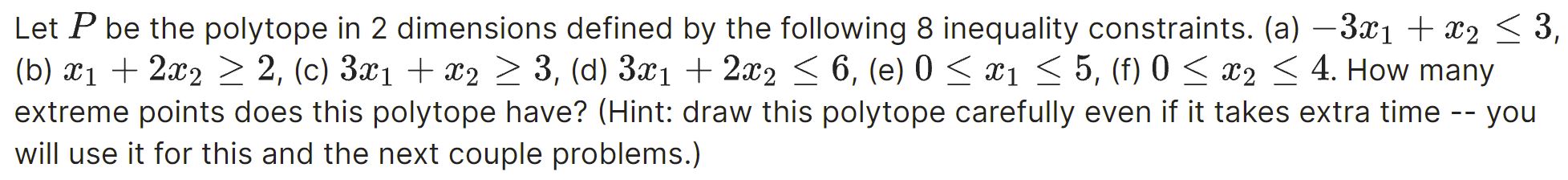
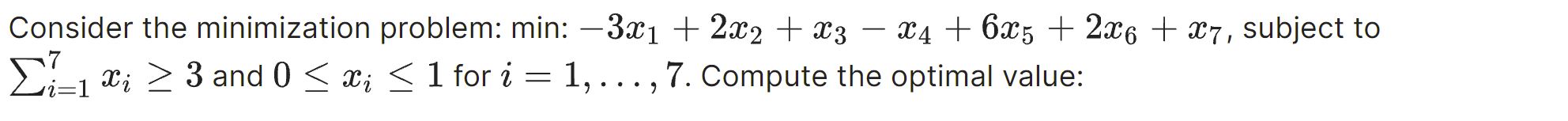
Let P be the polytope in 2 dimensions defined by the following 8 inequality constraints. (a) 3m1 + mg g 3, (b) $1 + 23:2 2 2, (G) 3:61 + 3:2 2 3, (d) 3331 + 2.782 g 6, (e) 0 3 1:1 3 5, (f) 0 g 932 S 4. How many extreme points does this polytope have? (Hint: draw this polytope carefully even if it takes extra time you will use it for this and the next couple problems.) For one last time, consider again the same polytope P. For the previous two problems, the LPs defined had a unique solution. Find a value of 62 E [0, 1/2] so that there are infinitely many solutions to the problem: min: 131 + an over P. Consider again the same polytope P defined in Problem 4, and consider the optimization problem: min: .761 -l- 021:2 over P. When (:2 = 1/2, we have the problem from the previous problem. Solve it again, but this time for (:2 = 0. Consider the minimization problem: min: 3x1 -| 21232 + m3 $4 + 621:5 + 2:135 + 337, subject to 57:1 mi 2 3 and 0 3 am