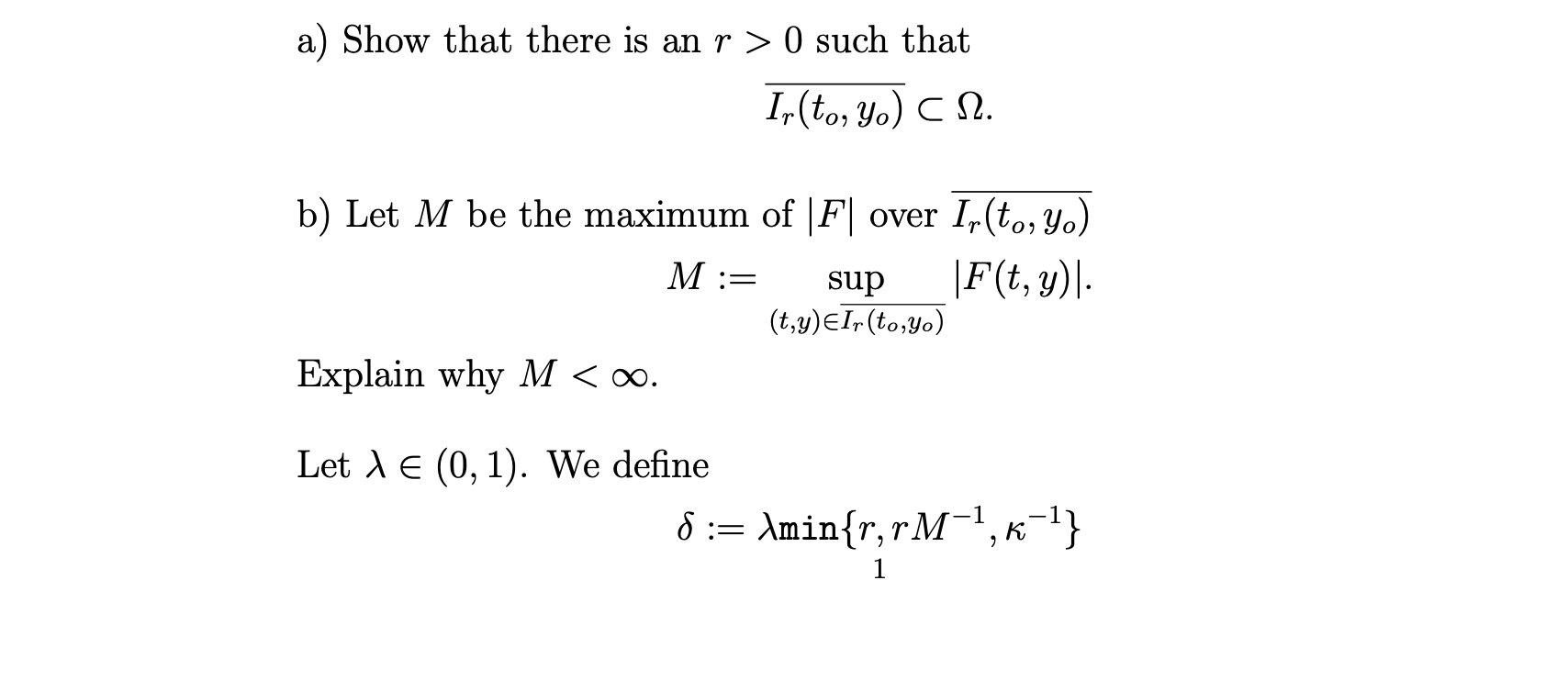
Let Q C R? be a nonempty open set. Let (t,,7,) Q Let F: Q=R be a continuous function on 2 satisfying IF(tu) F(t, 1)) 0 and a differentiable function y:[=0+toto+6 >R satisfying (k) (1) (t,y(t)) Qforallt [d+1t,t,+ ] (2) y(t) = F(t,y(t)) and y(to) = Yo. a) Show that there is an r > 0 such that Ir (to, yo) Cn. b) Let M be the maximum of | F| over Ir(to, y.) M : = sup IF (t, y)l. (t,y) EIr (to,yo) Explain why M