Question: Let R be a commutative ring with multiplicative identity 1 # 0. Call an ideal I in R prime if for any x,y R with

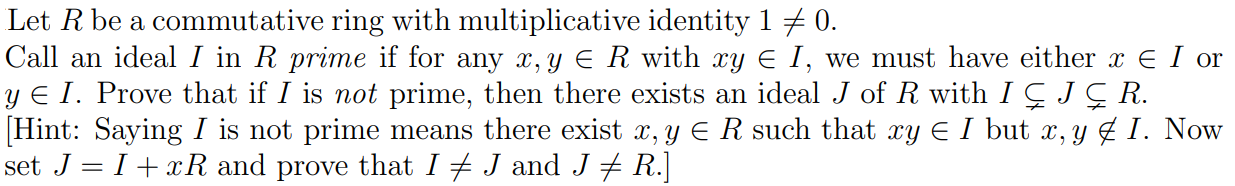
Let R be a commutative ring with multiplicative identity 1 # 0. Call an ideal I in R prime if for any x,y R with xzy I, we must have either x I or y I. Prove that if I is not prime, then there exists an ideal J of R with I C J C R. [Hint: Saying [ is not prime means there exist z,y R such that zy I but =,y I. Now set J = I + xR and prove that I # J and J # R.]

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

if do - a, + a2 - . . . (-1)*a, is divisible by 11. 33. Show that the number 7, 176,825,942, 116,027,211 is divisible by 9 but not divisible by 11. 34. Show that the number 9,897,654,527,609,805 is...

How we proceed f(1). Find a polynomial g(x) in Z[x] such that Ker d = (g(x)). Is there more than one possibility for g(x)? To what familiar ring is Z[x]/Ker o isomorphic? Do this exercise with Z...

Give a one- or two-sentence synopsis of "if' part of Theorem 27.9. Data from Theorem 27.9 Let R be a commutative ring with unity. Then M is a maximal ideal of R if and only if R/M is a field. Proof...

1. Find an integer n that shows the rings Z, need not have the following properties that the ring of integers has. a) as = a implies a = 0 or a = 1 b) ab = 0 implies a = 0 or b = 0 c) ab = ac and a #...

Give a one- or two-sentence synopsis of "only if' part of Theorem 27.9. Data from Theorem 27.9 Let R be a commutative ring with unity. Then M is a maximal ideal of R if and only if R/M is a field....

Math 113 Pierre Simon pierre.simon@berkeley.edu Homework 10 due November 22 Reading assignment: Read the chapters on euclidean rings and PID. Problem 1 Let R be a principal ideal domain (PID) and let...

1. (10+5 pts) (a) Let / and J be two left ideals of R and let It J = {xty : re l, ye J}. Prove that I + J is a left ideal of R. (b) Formulate and prove an analogous statement for two-sided ideals. 2....

6. List all the polynomials of degree 2 in Zz[x]. Which of these are equal as functions from Z2 to Zz? 7. Find two distinct cubic polynomials over Z2 that determine the same function from Zz to Z2....

Modern algebra: well written and well explanatory pls Let R be a commutative ring wilk identity, I an ideal of R and AIR- R/ I the canonical projection . a If S is a multiplicative subset of R, then...

Question 1 Let R denote a commutative ring, and let I, P R with I P. Show that P is prime in R if and only if P/I is prime in R/I. Question 2 Let R be an integral domain. Prove that if every ideal of...

Let f := R R and let R. Show that limf(x + c) = L.

A study was performed to investigate the shear strength of soil (y) as it related to depth in feet (x1) and moisture content (x2). Ten observations were collected, and the following summary...

Book value provides a useful benchmark in the Price to Book ratio, because a . book value includes a current assessment by investors of the firm's future prospects b . book value is more volatile...

The following information applies to the questions displayed below.] Delph Company uses a job-order costing system and has two manufacturing departments-Molding and Fabrication. The company provided...