Question: Let R be a ring. (a) Show that nil(R) is an ideal of R. (b) Show that nil( Ril(R)) = 0. Definition. Let R be

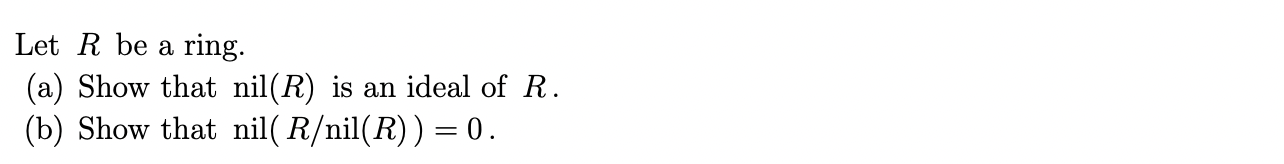
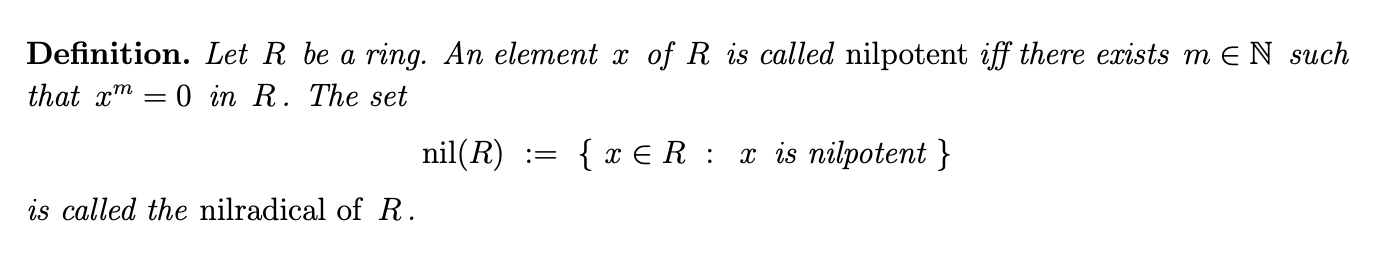
Let R be a ring. (a) Show that nil(R) is an ideal of R. (b) Show that nil( Ril(R)) = 0. Definition. Let R be a ring. An element x of R is called nilpotent iff there exists m E N such that xm = 0 in R. The set nil(R) := {xER : x is nilpotent} is called the nilradical of R

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

solve these following 17. Show that 0 is the only nilpotent element in an integral domain. 18. A ring element a is called an idempotent if a2 = a. Prove that the only idempotents in an integral...

help me Finance Suppose you have bought a put option to sell with an exercise price of $50 per share for 100 shares over next 4 month trading at $3. a. draw the put and profit digram? +art b. what...

Definition: A ring is a set A, equipped with two operations 1. Addition: + : R x R -> R, 2. Multiplication: . : R x R - R. such that the following axioms are satisfied: 1. For all a, be R, atb=bta....

Definition: A ring is a set R, equipped with two operations 1, Addition: + : R x R - R 2. Multiplication: . : R x R - R, such that the following axioms are satisfied: 1. For all a, bE R, a + b= btu....

Help pls 29. In Z[x], the ring of polynomials with integer coefficients, let / = (f(x) E Z[x] If(0) = 0}. Prove that I = (x). (This exercise is re- ferred to in this chapter and in Chapter 15.) 30....

Let R be any ring (possibly without identity) and Fa free R-module on the set X, with L : X F, as in Exercise 2. Show that L (X) is a set of generators of the R-module F. is commutative. Conclude...

Could you explain how to show 10.2 Definition 10.1. Let R be a ring. Then a polynomial with coefficients in R is a formal expression do + aix + azx2 + ... + anx", where a; E R and n is a nonnegative...

This is for abstract algebra class. Please show me all the details from scratch please. Thank you. 6. Let R be a ring with more than one element such that for each nonzero a R, there exists a unique...

Let R be any ring (possibly without identity) and X a nonempty set. In this exercise an R-module Fis called a free module on X if F is a free object on X in the category of a/I left R-modules. Thus...

Let : R R' be a ring homomorphism and let N be an ideal of R. a. Show that [N] is an ideal of [R]. b. Give an example to show that [N] need not be an ideal of R'. c. Let N' be an ideal either of...

Express the answer for 3.445 + 90.83 72.4 to the proper number of significant figures.

Find Io in the network in figure using Thevenin?s theorem, 4 kn 2 mA 3 kn 12 v(+ 6 kn 2 kn

La empresa Debo Estudiar ha preparado su estado anual de resultados, presupuestado, como sigue. Reformule el estado anual de resultados sobre una base del margen de contribucin. Ventas (200 000...

CUNY Corp. has just signed a lease for its new manufacturing facility. The lease agreement calls for annual payments of$1,450,000 for30 years with the first payment due today. If the interest rate...