Question: Let R be a ring. An element a: E R is nilpotent if cc = 0 for some positive integer n. (a) Assume that R

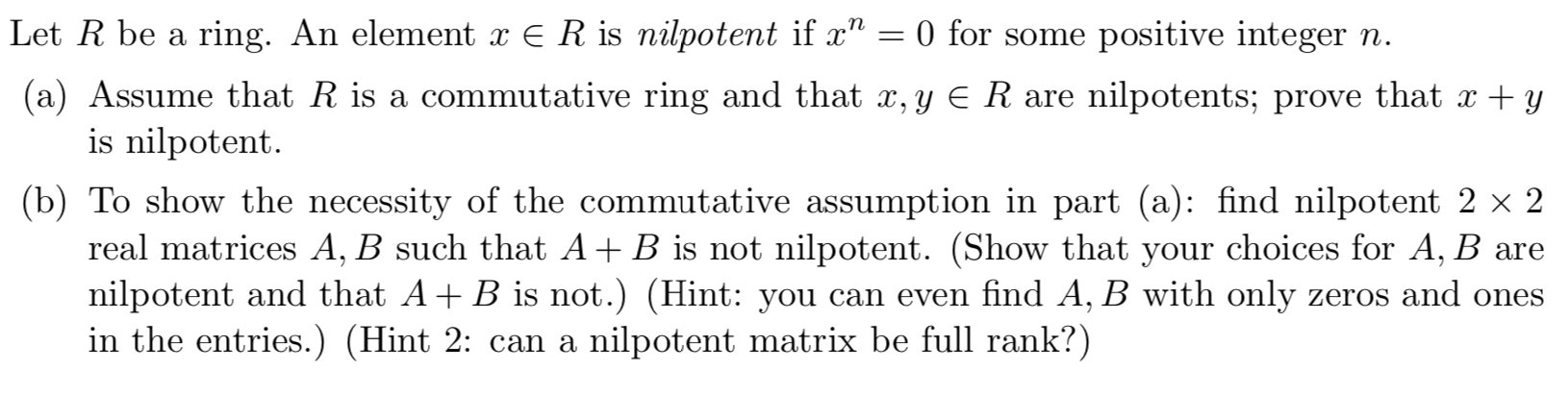
Let R be a ring. An element a: E R is nilpotent if cc\" = 0 for some positive integer n. (a) Assume that R is a commutative ring and that 11:, y E R are nilpotents; prove that x + y is nilpotent. (b) To show the necessity of the commutative assumption in part (a): nd nilpotent 2 x 2 real matrices A, B such that A + B is not nilpotent. (Show that your choices for A, B are nilpotent and that A + B is not.) (Hint: you can even nd A, B with only zeros and ones in the entries.) (Hint 2: can a nilpotent matrix be full rank?)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

solve these following 17. Show that 0 is the only nilpotent element in an integral domain. 18. A ring element a is called an idempotent if a2 = a. Prove that the only idempotents in an integral...

1. Find an integer n that shows the rings Z, need not have the following properties that the ring of integers has. a) as = a implies a = 0 or a = 1 b) ab = 0 implies a = 0 or b = 0 c) ab = ac and a #...

2.1. Let Sbeaset and A C Sx.S. Show that there is a unique equivalence relation R on S containing A which is minimal with respect to this property, i.e. A C R' and R' an equivalence relation implies...

Definition: A ring is a set A, equipped with two operations 1. Addition: + : R x R -> R, 2. Multiplication: . : R x R - R. such that the following axioms are satisfied: 1. For all a, be R, atb=bta....

Definition: A ring is a set R, equipped with two operations 1, Addition: + : R x R - R 2. Multiplication: . : R x R - R, such that the following axioms are satisfied: 1. For all a, bE R, a + b= btu....

Please solve it as fast as possible. Abstract Algebra 9. Let R be the ring Z50- (a) (3 PTS) Find an element of R which is a zero-divisor. (b) (3 PTS) Find an element of R which is a unit. (c) (3 PTS)...

Help pls 29. In Z[x], the ring of polynomials with integer coefficients, let / = (f(x) E Z[x] If(0) = 0}. Prove that I = (x). (This exercise is re- ferred to in this chapter and in Chapter 15.) 30....

Let R be a ring with identity, not necessarily commutative. An element e R is said to be idempotent if e^2 = e. 1) Let x R. Show that the set RxR = {rxs : r, s R} is an ideal in R. 2) Let R be...

Could you explain how to show 10.2 Definition 10.1. Let R be a ring. Then a polynomial with coefficients in R is a formal expression do + aix + azx2 + ... + anx", where a; E R and n is a nonnegative...

1. (10+5 pts) (a) Let / and J be two left ideals of R and let It J = {xty : re l, ye J}. Prove that I + J is a left ideal of R. (b) Formulate and prove an analogous statement for two-sided ideals. 2....

Write an equation describing the radioactive decay of each of the following nuclides. b. Li (B followed by a) c. 4Be (electron capture) d. B (positron)

You are provided with the following information for Lily Inc. for the month ended June 30, 2020. Lily uses the periodic method for inventory. Date Description Quantity Unit Cost or Selling Price June...

Most companies pay current liabilities Select an answer and submit. For keyboard navigation, use the up / down arrow keys to select an answer. a by creating long - term liabilities. b by issuing...

please answer only if you know programming language is c++ For this lab, your objective is to define the functions below. Define the void function SwapNodes () that takes three generic type Node...