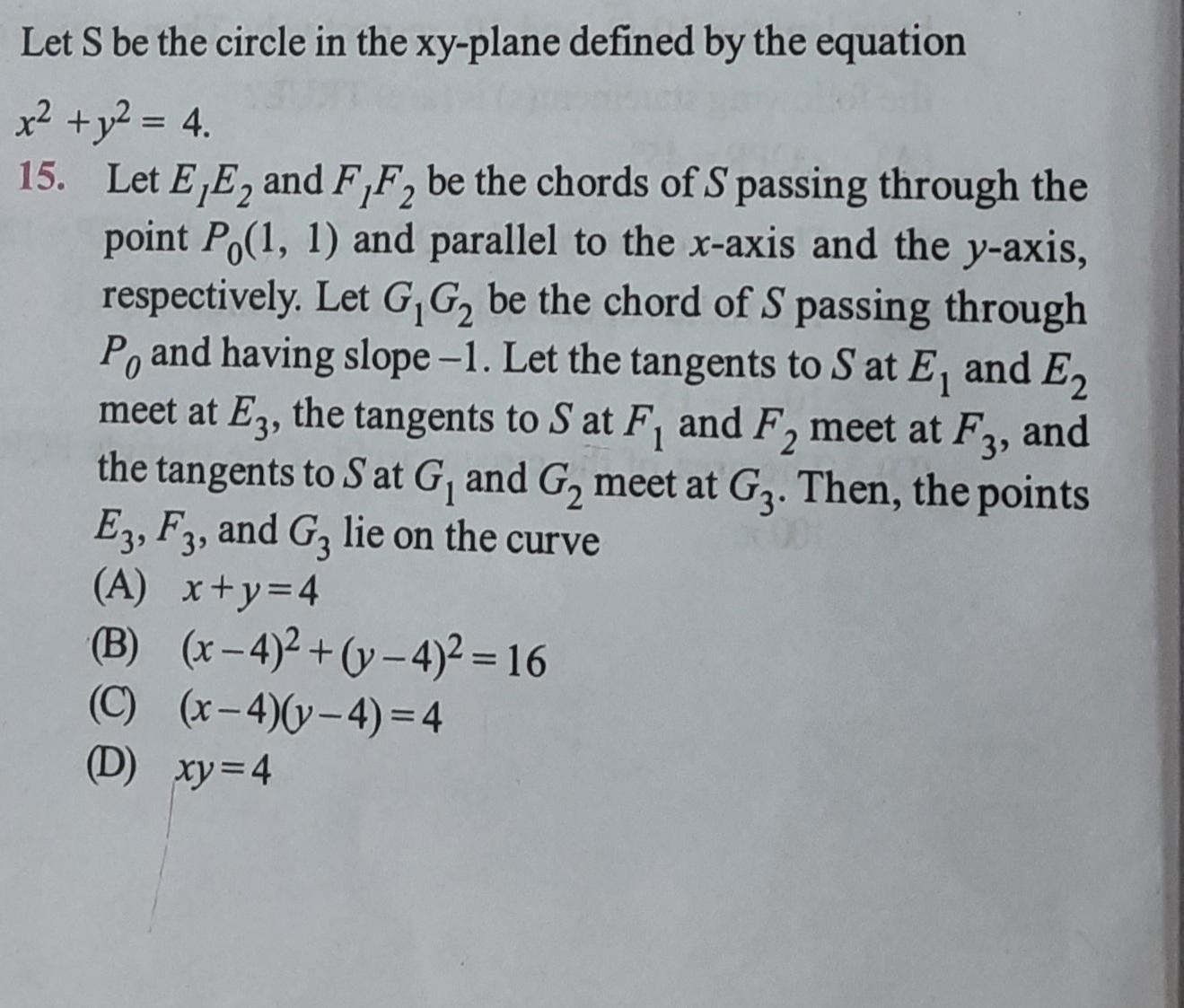
Let S be the circle in the xy-plane defined by the equation x + y = 4. Let E,E and F,F be the chords of S passing through the point Po(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G G be the chord of S passing through Po and having slope-1. Let the tangents to Sat E and E2 meet at E3, the tangents to S at F and F meet at F3, and the tangents to Sat G and G meet at G3. Then, the points E3, F3, and G3 lie on the curve (A) x+y=4 1 (B) (x-4)+(y-4) = 16 (C) (x-4)(y-4)=4 (D) xy=4