Let S be the initial state and G be the (only) goal state in the following graph 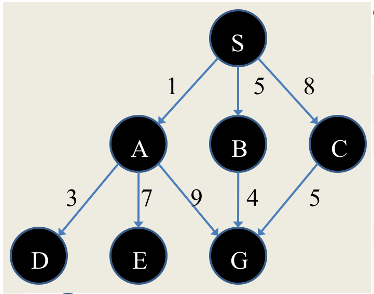Apply Uniform-Corst Search as implemented via best-first search to compute a solution path.

NOTE: Add nodes to the frontier such that the preferred expansion is given "from left to the right" when multiple nodes with same evaluation function value are added.

Tasks

For a node n, let f(n) be the evaluation function value and c(n) the path cost of that node.

1. Show for each removal of a node from the frontier,

a) the frontier with elements of the form " n : (f(n),c(n)) ",

b) the list of reached states of the form "s : minimal path cost to s"

c) the list of visited states of the form "s: path cost of s".

2. Provide the resulting solution path as well as the path cost of the resulting solution path.