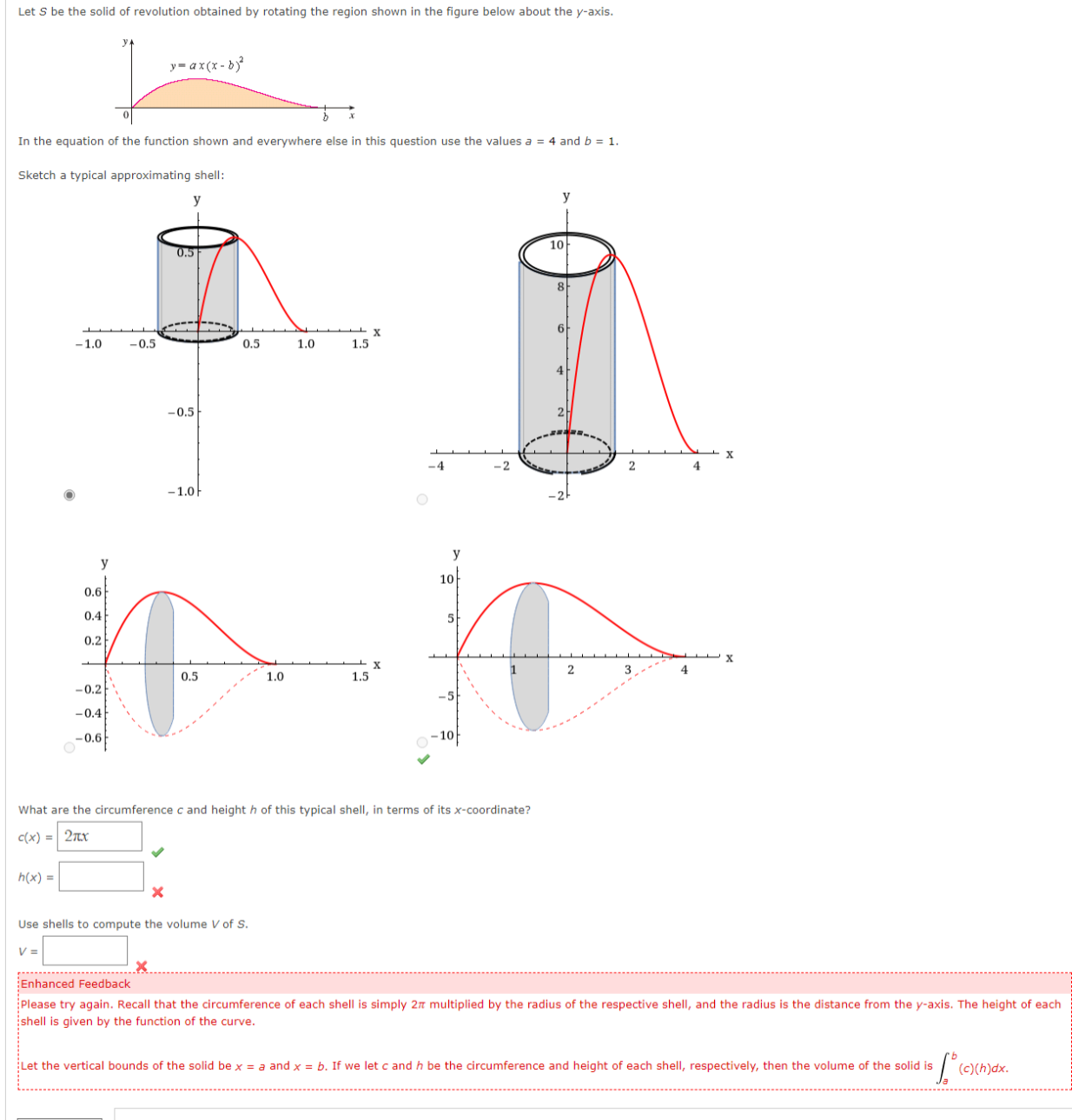
Let S be the solid of revolution obtained by rotating the region shown in the figure below about the y-axis. y = ax(x - b) In the equation of the function shown and everywhere else in this question use the values a = 4 and b = 1. Sketch a typical approximationg shell: 0.5 10 8 -1.0 -0.5 0.5 1.0 1.5 - 0.5 2H -4 - 2 2 -1.0 O -2/ 10 0.6 0.2 X 05 1.0 1.5 2 -0.2 -5 -0.4 -0.6 -10 What are the circumference c and height h of this typical shell, in terms of its x-coordinate? c(x) = 2nx h ( x ) = Use shells to compute the volume V of S. V= Enhanced Feedback Please try again. Recall that the circumference of each shell is simply 27 multiplied by the radius of the respective shell, and the radius is the distance from the y-axis. The height of each shell is given by the function of the curve. Let the vertical bounds of the solid be x = a and x = b. If we let c and h be the circumference and height of each shell, respectively, then the volume of the solid is / (c)(hidx