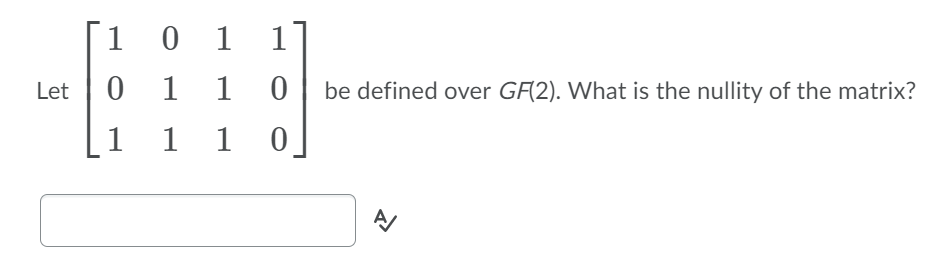
Question: Let T 2 R2 > R2 be a linear transformation given by Tiiii) = [1:33] wherep is a real number. ( i 1 i i





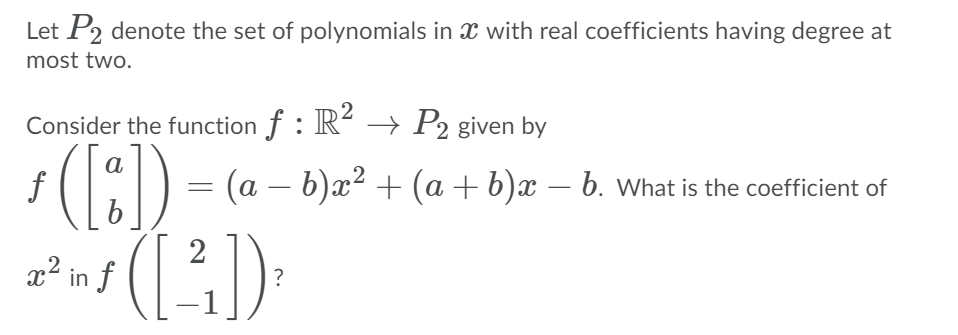


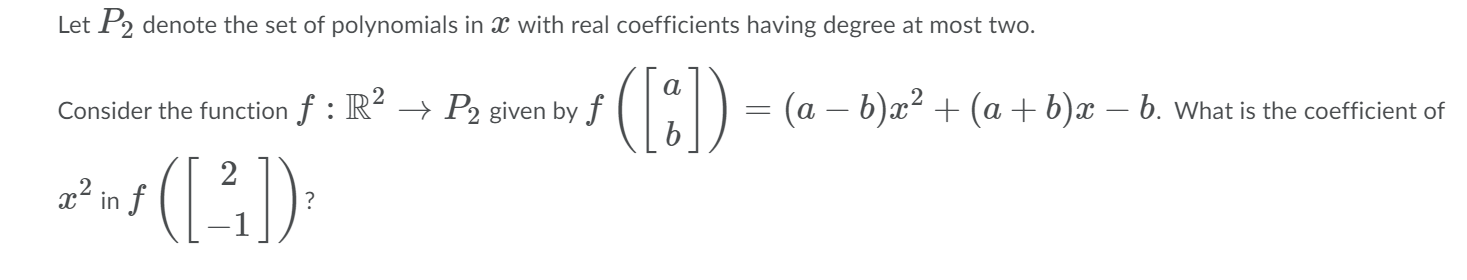




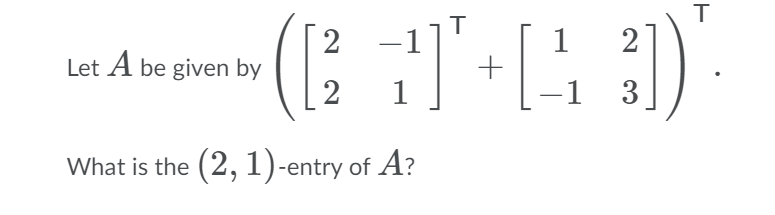
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


