Let T be a binary tree with nnodes, and let f() be the level numbering

function of the positions of T, as given in Section 8.3.2. a. Show that, for every position pof T, f(p) 2n2. ( n is the number of nodes in the

binary tree) b. Show an example of a binary tree with seven nodes that attains the above upper bound on

f(p) for some position p.

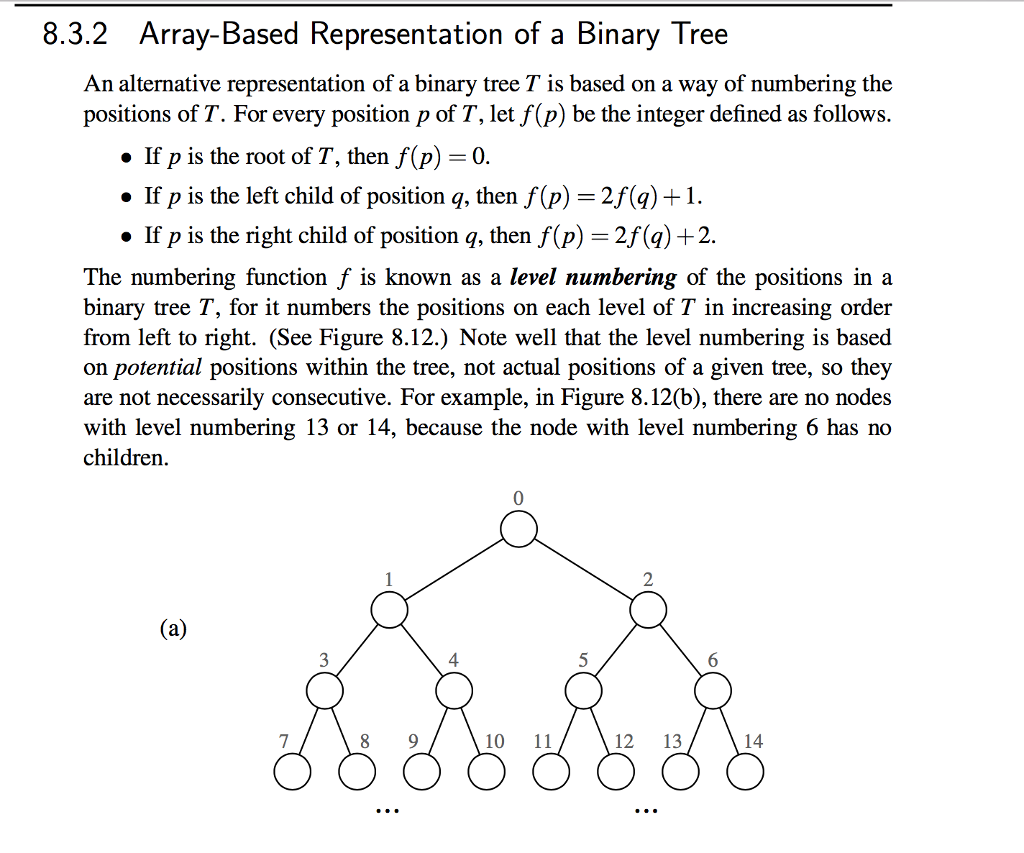
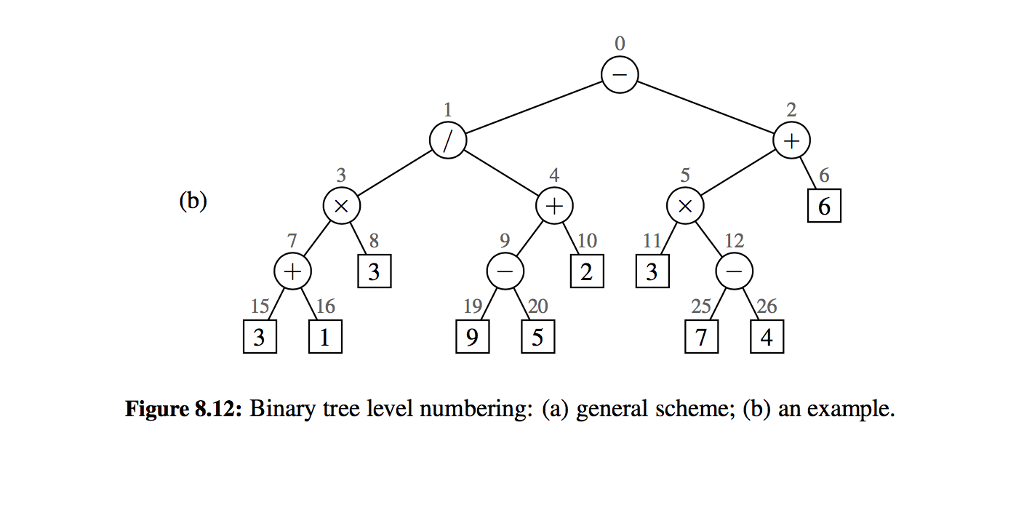
8.3.2 Array-Based Representation of a Binary Tree An alternative representation of a binary tree Tis based on a way of numbering the positions of T. For every position p of T, let f(p) be the integer defined as follows. If p is the root of T, then f(p) 0. If p is the left child of position q, then f 2f(q) 1. If p is the right child of position q, then f (p) 2f (q) +2. The numbering function f is known as a level numbering of the positions in a binary tree T, for it numbers the positions on each level of T in increasing order from left to right. (See Figure 8.12.) Note well that the level numbering is based on potential positions within the tree, not actual positions of a given tree, so they are not necessarily consecutive. For example, in Figure 8.12 b), there are no nodes with level numbering 13 or 14, because the node with level numbering 6 has no children. (a) 10 11 12 13 14