Question: Let T be a fiul 3-ary tree. That is, each internal (branch) node has exactly three children, each external (leaf) node has zero children (as

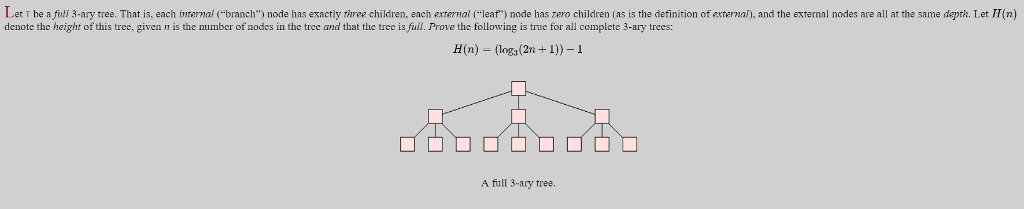
Let T be a fiul 3-ary tree. That is, each internal

Let T be a fiul 3-ary tree. That is, each internal ("branch") node has exactly three children, each external ("leaf") node has zero children (as is the definition of external), and the external nodes are all at the same depth. Let TT(n) denote the height of this tree, given n is the number of nodes in the tree and that the tree is full. Prove the following is true for all complete 3-ary trees: H(n) - (log,(2n +1))-1 A full 3-ary tree

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Consider two cases involving parallel flow of dry air at V = 1 m/s, T = 45C, and atmospheric pressure over an isothermal plate at T s = 20C. In the first case, Re x.c = 5 x 10 5 , while in the...

Help! Data Structure problem List.java import java.util.Random; import java.util.function.BiFunction; import java.util.function.Function; class EmptyListE extends Exception {} abstract class List {...

Data Structure problem List.java import java.util.Random; import java.util.function.BiFunction; import java.util.function.Function; class EmptyListE extends Exception {} abstract class List { static...

A feckless tree is a 3-ary rooted tree where nodes are labeled with pairs of integers and that satisfies the following properties: a) If n is a leaf, then n is labeled (4,7) or (7,12) bj No internal...

"Fortran, Algol and Lisp invented most programming language concepts 50 years ago; adding the concept of object-orientation suffices to explain all programming languages to date". To what extent is...

you are asked to assemble a proof by induction from the parts given. you pick one from each letter. answer should be like this: (e.g., A5 B2 C3 D4 E1 F2 G3 H5 I3). Question 1 Definition: We define a...

Have a C compiler which is ANSI conforming in all respects except that it has no facility for the definition, declaration or use of standard C structures. Outline a set of routines written in this...

2. Induction Proof correctness (10 pts) Recall that a full binary tree contains (A) just a single leaf node, or (B) is an internal node (the root) connected to two disjoint subtrees, which are...

Does this proof have a flaw, if so explain the flaw in the proof. Proof? By induction on number of internal nodes. For2 0, let IH(n) be the statement: "all full binary trees having exactly n internal...

In the following question, you are asked to assemble a proof by induction from the parts given. Your answer should include one paragraph from each letter prefix. The answer should only include the...

The most recent annual dividend payment of Warren Industries, a rapidly growing boat manufacturer, was $1.50 per share. The firms financial manager expects that these dividends will increase by 10%...

Explain in your own words implementation of Euler-tour trees in functional programming ?

Which statement best describes the average profitability ( rate of return on sales ) of Coors for the period 1 9 8 1 1 9 8 5 ? Coors s profitability ( ROS ) is exactly equal to that of its industry...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

12. Detailed lesson plans have important information for trainers. List the different types of information found in a detailed lesson plan. Also, indicate the importance of each type of information...

10. What learning conditions are necessary for short- and long-term retention of training content to occur?

13. What is a design document? What is included in a design document? How is it useful for training?