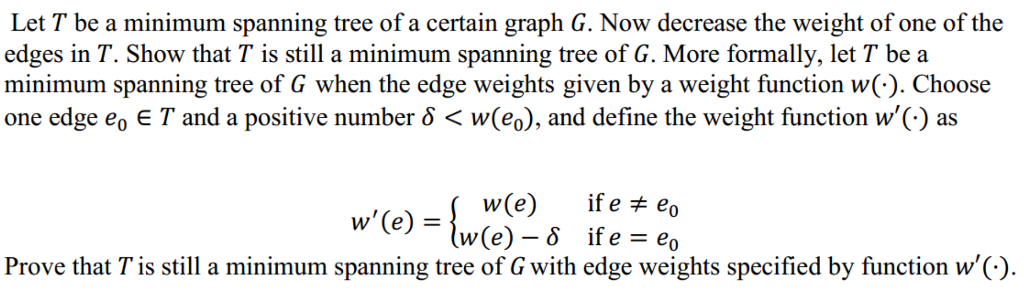
Let T be a minimum spanning tree of a certain graph G. Now decrease the weight of one of the edges in T. Show that T is still a minimum spanning tree of G. More formally, let T be a minimum spanning tree of G when the edge weights given by a weight function w(). Choose one edge eo E T and a positive number w(eo), and define the weight function w'(.) as w'(e) ={w(e) if e te, Prove that Tis still a minimum spanning tree of G with edge weights specified by function w'(.)