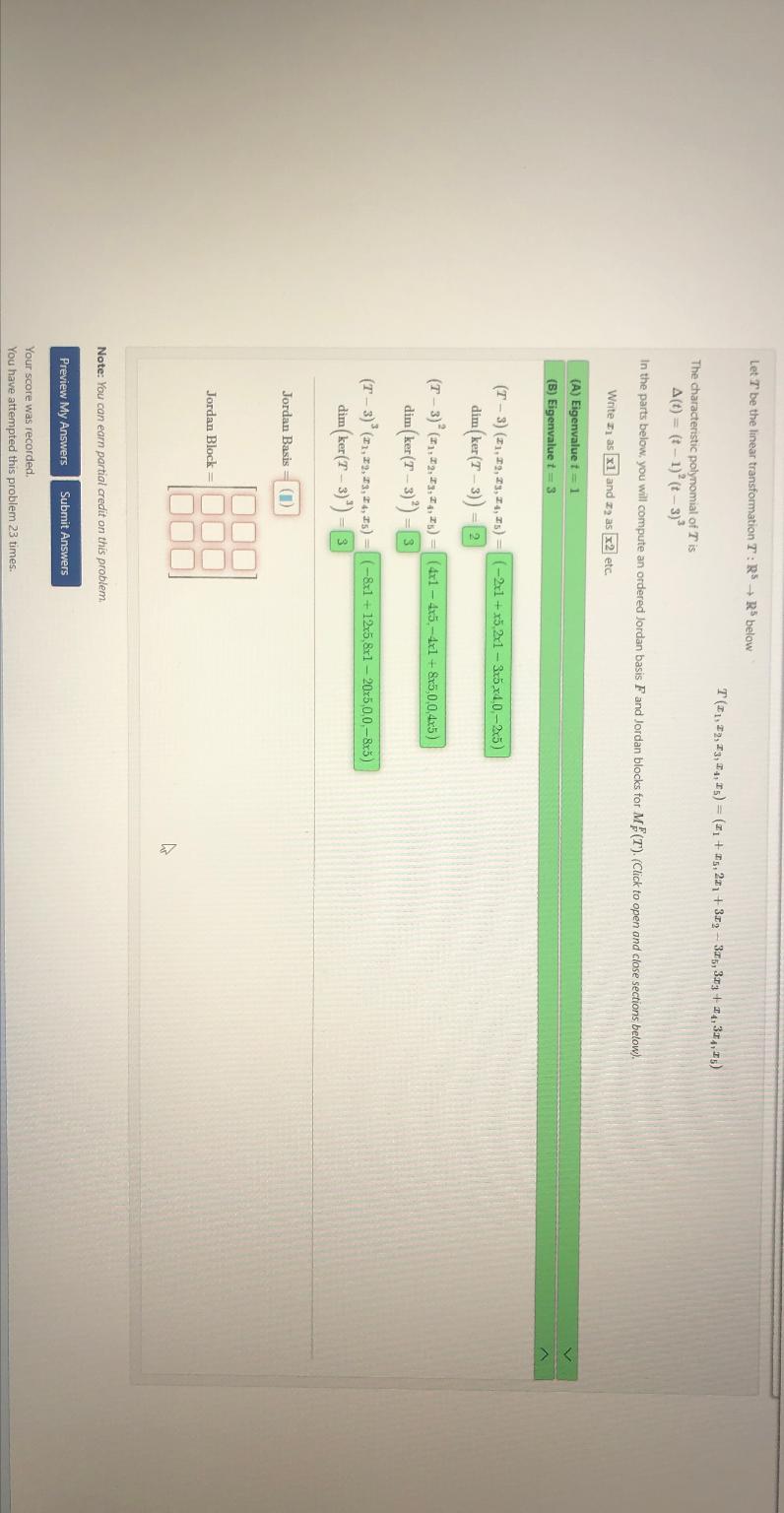
Let $T$ be the linear transformation $T$:$R^5{R}^5$ below

$T(x_1,x_2,x_3,x_4,x_5)=(x_1+x_5,2x_1+3x_2-3x_5,3x_3+x_4,3x_4,x_5)$

The characteristic polynomial of $T$ is

$(t)=(t-1{)}^2(t-3{)}^3$

In the parts below, you will compute an ordered Jordan basis $F$ and Jordan blocks for $M_F^F(T).($Click to open and close sections below$).$

Write $x_{1}asx1$ and $x_{2}asx2$ etc.

$($A$)$ Eigenvalue $t=1$

$($B$)$ Eigenvalue $t=3$

$(T-3)(x_1,x_2,x_3,x_4,x_5)=(-21+x5,21-354,0,-25)$

dim$(ker(T-3))=2$

$(T-3{)}^2(x_1,x_2,x_3,x_4,x_5)=(41-45,-41+85,0,0,45)$

dim$(ker(T-3{)}^2)=3$

$(T-3{)}^3(x_2,x_2,x_3,x_4,x_5)=(-81+125,81-205,0,0,-85)$

dim$(ker(T-3{)}^3)=3$

Jordan Basis $=($II$)$

Note: You can earn partial credit on this problem.

Preview My Answers

Submit Answers

Your score was recorded.

You have attempted this problem $23$ times.