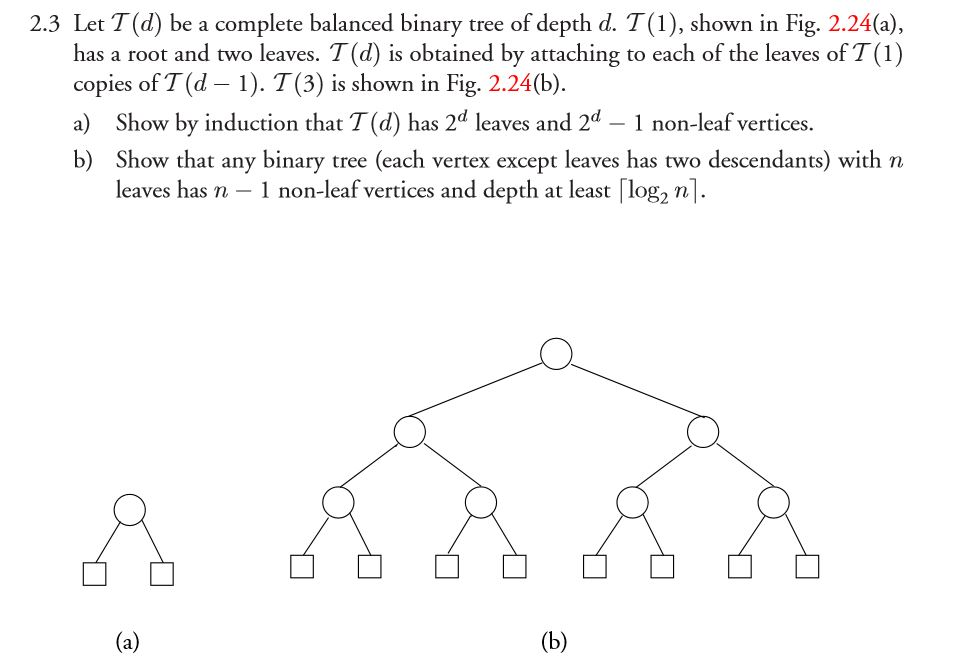
Let T(d) be a complete balanced binary tree of depth d. T(1), shown in Fig. 2.24(a), has a root and two leaves. T(d) is obtained by attaching to each of the leaves of T (1) copies of T (d - 1). T(3) is shown in Fig. 2.24(b). a) Show by induction that T(d) has 2^d leaves and 2^d - 1 non-leaf vertices. b) Show that any binary tree (each vertex except leaves has two descendants) with n leaves has n - 1 non-leaf vertices and depth at least [log_2 n]