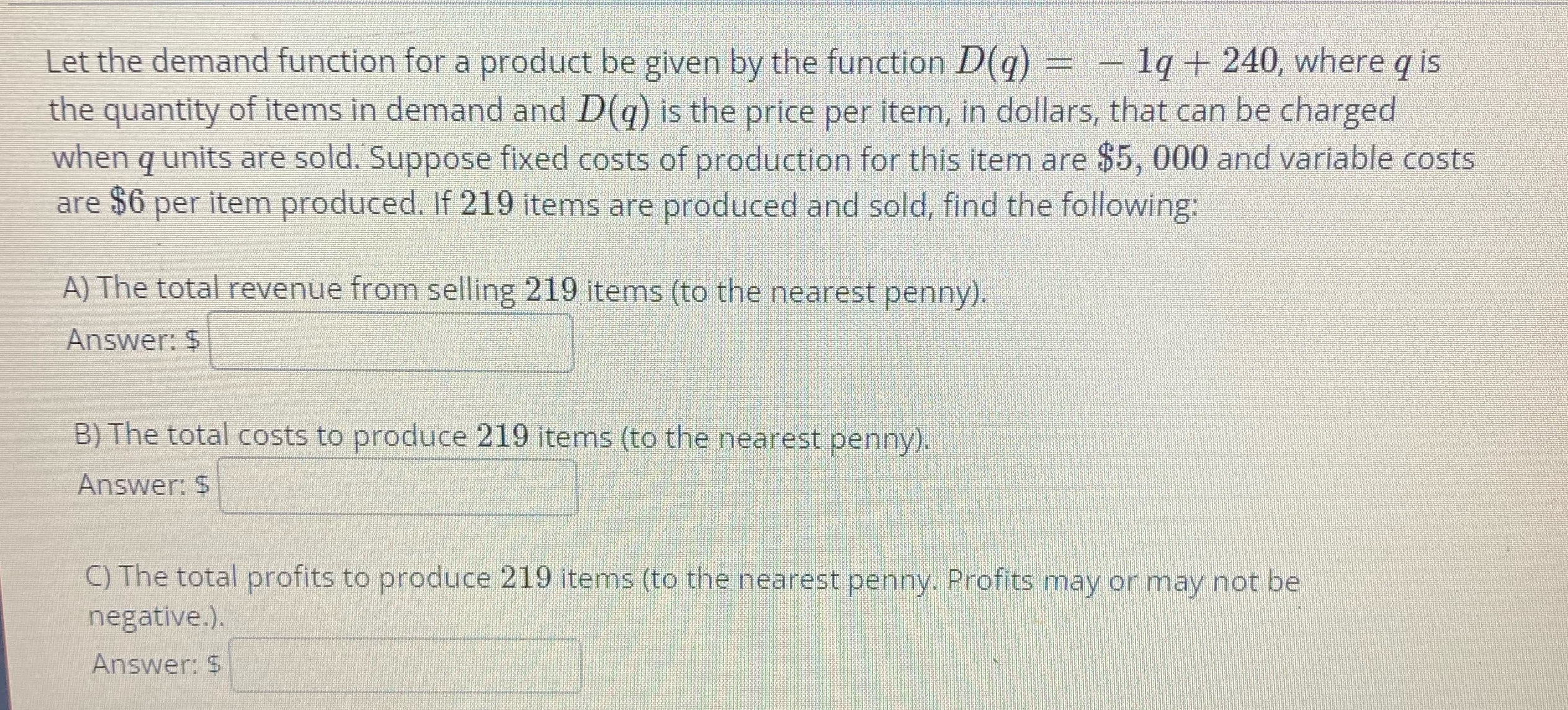
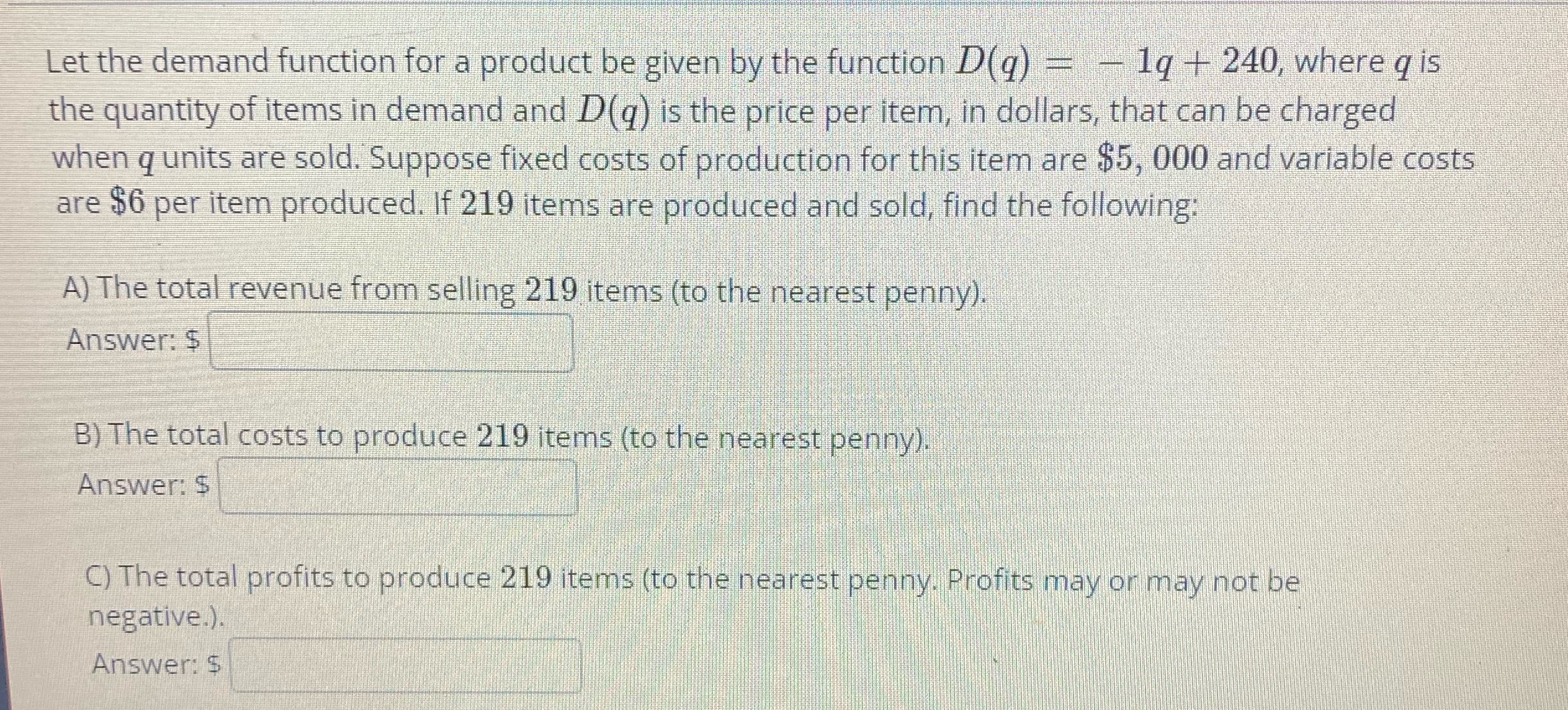
Let the demand function for a product be given by the function D(q) = - 1q + 240, where q is the quantity of items in demand and D(q) is the price per item, in dollars, that can be charged when q units are sold. Suppose fixed costs of production for this item are $5, 000 and variable costs are $6 per item produced. If 219 items are produced and sold, find the following: A) The total revenue from selling 219 items (to the nearest penny). Answer: $ B) The total costs to produce 219 items (to the nearest penny). Answer: $ C) The total profits to produce 219 items (to the nearest penny, Profits may or may not be negative.). Answer: $