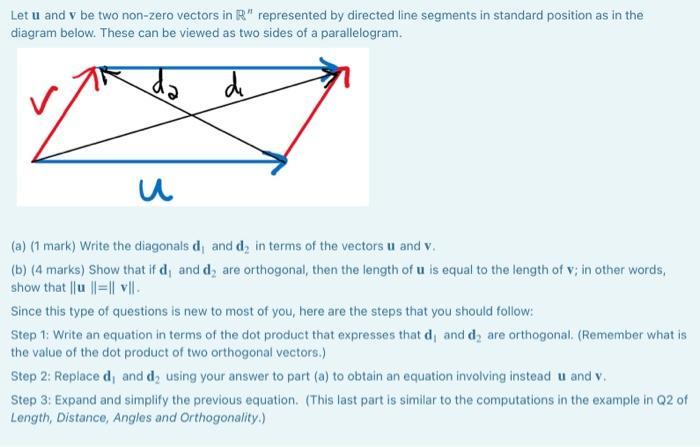
Let u and v be two non-zero vectors in R" represented by directed line segments in standard position as in the diagram below. These can be viewed as two sides of a parallelogram. da de (a) (1 mark) Write the diagonals d, and d in terms of the vectors u and v. (b) (4 marks) Show that if d, and d are orthogonal, then the length of u is equal to the length of v; in other words, show that ||u ||=|| v||. Since this type of questions is new to most of you, here are the steps that you should follow: Step 1: Write an equation in terms of the dot product that expresses that d, and d are orthogonal. (Remember what is the value of the dot product of two orthogonal vectors.) Step 2: Replace d, and d using your answer to part (a) to obtain an equation involving instead u and v. Step 3: Expand and simplify the previous equation. (This last part is similar to the computations in the example in Q2 of Length, Distance, Angles and Orthogonality.)