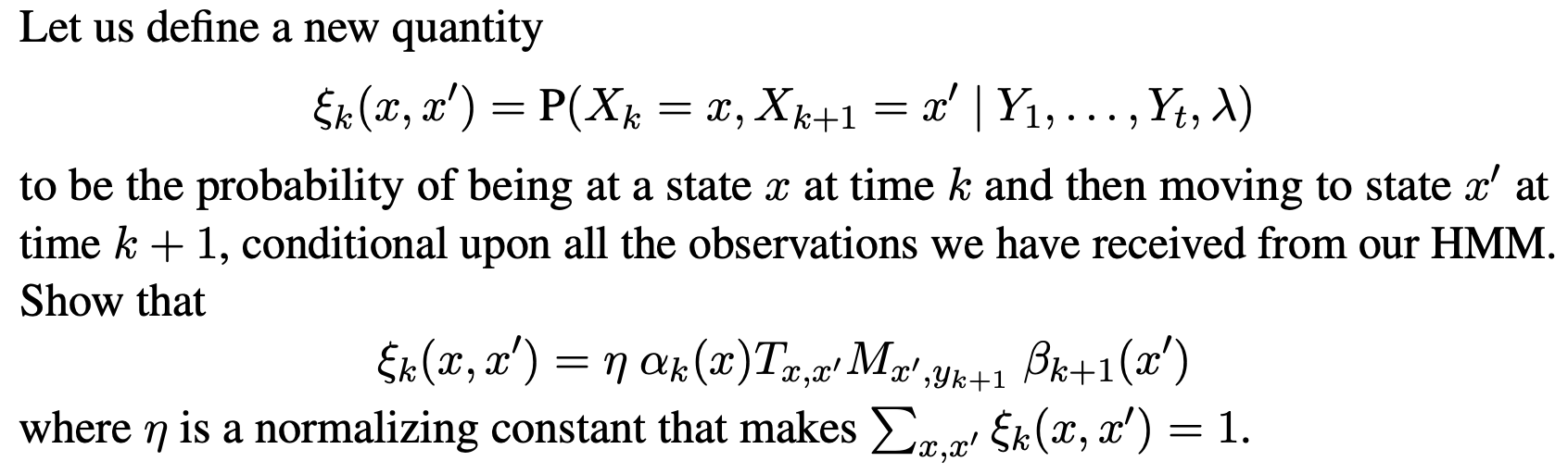
Let us define a new quantity k (x, x') = P(Xk = x, Xk+1 = x' | Y,..., Yt, ) to be the probability of being at a state x at time k and then moving to state x' at time k + 1, conditional upon all the observations we have received from our HMM. Show that k (x, x') = k (x)T nk(x)Tx,x' Mx' x,x' Mx',Yk+1 Bk+1(x') where n is a normalizing constant that makes x,x' (k(x, x') = 1.